
【题目】(1)证明推断:如图(1),在正方形ABCD中,点E,Q分别在边BC,AB上,DQ⊥AE于点O,点G,F分别在边CD,AB上,GF⊥AE.
①求证:DQ=AE;
②推断:![]() 的值为 ;
的值为 ;
(2)类比探究:如图(2),在矩形ABCD中,![]() =k(k为常数).将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形FEPG,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;
=k(k为常数).将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形FEPG,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;
(3)拓展应用:在(2)的条件下,连接CP,当k=![]() 时,若tan∠CGP=
时,若tan∠CGP=![]() ,GF=2
,GF=2![]() ,求CP的长.
,求CP的长.

【答案】(1)①见解析;②1;(2)![]() =k,见解析;(3)PC=
=k,见解析;(3)PC=![]() .
.
【解析】
(1)①由正方形的性质得AB=DA,∠ABE=90°=∠DAQ.所以∠QAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠QAO=∠ADO,于是△ABE≌△DAQ,可得AE=DQ.
②证明四边形DQFG是平行四边形即可解决问题.
(2)结论:![]() .如图2中,作GM⊥AB于M.证明△ABE∽△GMF即可解决问题.
.如图2中,作GM⊥AB于M.证明△ABE∽△GMF即可解决问题.
(3)如图2中,作PM⊥BC交BC的延长线于M.利用相似三角形的性质求出PM,CM即可解决问题.
(1)①证明:∵四边形ABCD是正方形,
∴AB=DA,∠ABE=90°=∠DAQ.
∴∠QAO+∠OAD=90°.
∵AE⊥DQ,
∴∠ADO+∠OAD=90°.
∴∠QAO=∠ADO.
∴△ABE≌△DAQ(ASA),
∴AE=DQ.
②结论:![]() .
.
理由:∵DQ⊥AE,FG⊥AE,
∴DQ∥FG,
∵FQ∥DG,
∴四边形DQFG是平行四边形,
∴FG=DQ,
∵AE=DQ,
∴FG=AE,
∴![]() ,
,
故答案为:1;
(2)结论:![]() .
.
理由:如图2中,作GM⊥AB于M.

∵AE⊥GF,
∴∠AOF=∠GMF=∠ABE=90°,
∴∠BAE+∠AFO=90°,∠AFO+∠FGM=90°,
∴∠BAE=∠FGM,
∴△ABE∽△GMF,
∴![]() ,
,
∵∠AMG=∠D=∠DAM=90°,
∴四边形AMGD是矩形,
∴GM=AD,
∴![]() .
.
(3)如图2中,作PM⊥BC交BC的延长线于M.
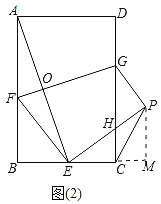
∵FB∥GC,FE∥GP,
∴∠CGP=∠BFE,
∴tan∠CGP=tan∠BFE=![]() ,
,
∴假设BE=3m,BF=4m,EF=AF=5m,
∵![]() ,FG=2
,FG=2![]() ,
,
∴AE=3![]() ,
,
∴BE2+AB2=AE2,
∴(3m)2+(9m)2=(3![]() )2,
)2,
∴m=1或﹣1(舍弃),
∴BE=3,AB=9,
∵BC:AB=2:3,
∴BC=6,
∴BE=CE=3,AD=PE=BC=6,
∵∠EBF=∠FEP=∠PME=90°,
∴∠FEB+∠PEM=90°,∠PEM+∠EPM=90°,
∴∠FEB=∠EPM,
∴△FBE∽△EMP,
∴![]() ,
,
∴![]() ,
,
∴EM=![]() ,PM=
,PM=![]() ,
,
∴CM=EM﹣EC=![]() ﹣3=
﹣3=![]() ,
,
∴PC= .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】长沙市教育局组织部分教师分别到A、B、C、D四个地方进行课程培训,教育局按定额购买了前往四地的车票,如图1是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
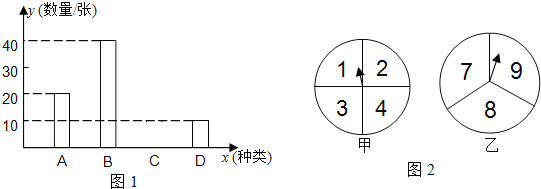
(1)若去A地的车票占全部车票的20%,求去C地的车票数,并补全条形统计图(图1);
(2)请从小到大写出这四类车票数的数字,并直接写出这四个数据的平均数和中位数;
(3)如图2,甲转盘被分成四等份且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,具体规定是:同时转动两个转盘,当指针指向的两个数字之和是偶数时,李老师出去培训,否则张老师出去培训(指针指在线上重转),试用“列表法”或“树状图”的方法分析这个规定对双方是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
(1)当⊙O的半径为2时,
①如果点A(0,1),B(3,4),那么d(A,⊙O)=_______,d(B,⊙O)= ________;
②如果直线![]() 与⊙O互为“可及图形”,求b的取值范围;
与⊙O互为“可及图形”,求b的取值范围;
(2)⊙G的圆心G在![]() 轴上,半径为1,直线
轴上,半径为1,直线![]() 与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=﹣x+b上,若矩形OCDB的面积为20,直线y1=2x+4与直线y2=﹣x+b交于点P.则P的坐标为( )
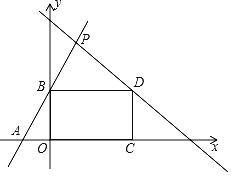
A.(2,8)B.![]() C.
C.![]() D.(4,12)
D.(4,12)
查看答案和解析>>
科目:初中数学 来源: 题型:
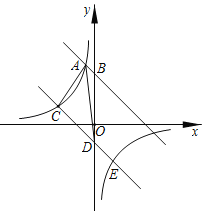
【题目】如图,在平面直角坐标系中,直线AB与y轴交于点![]() ,与反比例函数
,与反比例函数![]() 在第二象限内的图象相交于点
在第二象限内的图象相交于点![]() .
.
(1)求直线AB的解析式;
(2)将直线AB向下平移9个单位后与反比例函数的图象交于点C和点E,与y轴交于点D,求![]() 的面积;
的面积;
(3)设直线CD的解析式为![]() ,根据图象直接写出不等式
,根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在方格纸中,每个方格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图甲中,每个小正方形的边长为1,以线段AB为一边的格点三角形随着第三个顶点的位置不同而发生变化.
(1)根据图甲,填写下表,并计算出格点三角形面积的平均值;
格点三角形面积 | 1 | 2 | 3 | 4 |
频数 |
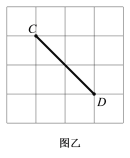
(2)在图乙中,所给的方格纸大小与图甲一样,如果以线段CD为一边,作格点三角形,试填写下表,并计算出格点三角形面积的平均值;
格点三角形面积 | 1 | 2 | 3 | 4 |
频数 |
(3)如果将图乙中格点三角形面积记为s,频数记为x,根据你所填写的数据,猜测s与x之间存在哪种函数关系,并求出函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克10元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中![]() ).
).
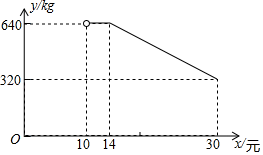
(1)直接写出y与x之间的函数关系式及自变量的取值范围.
(2)若农贸公司每天销售该特产的利润要达到3100元,则销售单价x应定为多少元?
(3)设每天销售该特产的利润为W元,若![]() ,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
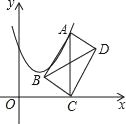
【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com