
分析 (1)要求出B地在A地何处,相距多少千米,只要将它所走的记录相加,如果是正数,就是B在A地的北方;如果是负数,就是B在A地的南方.它的绝对值就是A,B的距离;
(2)这一天共耗油=所走记录的绝对值的和×汽车每千米耗油升数.
解答 解:(1)-13+(-10)+8+(-14)+(-6)+13+(-6)+(-8)=-36(km).
答:B地在A地南方,相距36千米;
(2)(|-13|+|-10|+8+|-14|+|-6|+13+|-6|+|-8|)×0.5
=78×0.5
=39(升).
答:那么这一天共耗油39升.
点评 本题考查了正数和负数,利用了有理数的加法运算,根据题意列出算式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一长方形休闲场所的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为a米,宽为b米.
如图,在一长方形休闲场所的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为a米,宽为b米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
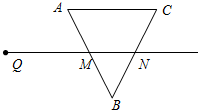 如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒).
如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com