
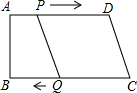
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.分析 (1)根据对边平行且相等的四边形是平行四边形列出方程,解方程即可;
(2)由AD∥BC,∠B=90°,可得当AP=BQ时,四边形ABQP是矩形,即可得方程:t=26-2t,解此方程即可求得答案.
解答 解:(1)当PD=CQ时,四边形PQCD为平行四边形,
即24-t=3t,
解得,t=6,
即当t=6s时,四边形PQCD为平行四边形;
(2)根据题意得:AP=tcm,CQ=3tcm,
∵AB=8cm,AD=24cm,BC=26cm,
∴DP=AD-AP=24-t(cm),BQ=26-3t(cm),
∵AD∥BC,∠B=90°,
∴当AP=BQ时,四边形ABQP是矩形,
∴t=26-3t,
解得:t=6.5,
即当t=6.5s时,四边形ABQP是矩形;
点评 此题考查了直角梯形的性质、平行四边形的判定、矩形的判定形的判定.熟练掌握平行四边形和矩形的判定,根据题意得出方程是解决问题的关键.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
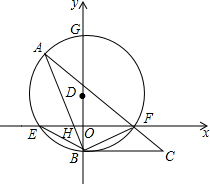 如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.
如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
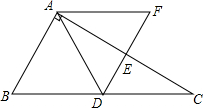 如图,Rt△ABC中,∠BAC=90°,∠C=30°.点D、E分别是边BC、AC的中点,DE的联线与BC的平行线AF交于点F.
如图,Rt△ABC中,∠BAC=90°,∠C=30°.点D、E分别是边BC、AC的中点,DE的联线与BC的平行线AF交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
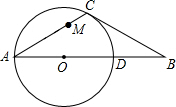 如图,在△ABC中,CA=CB,∠CAB=30°,⊙O经过点C,且圆的直径AD在线段AB上.
如图,在△ABC中,CA=CB,∠CAB=30°,⊙O经过点C,且圆的直径AD在线段AB上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
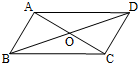 如图,在?ABCD中,AC=6,BD=10,
如图,在?ABCD中,AC=6,BD=10,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间 | 负责组别 | 车流总量 | 每分钟车流量 |
| 早晨上学6:30~7:00 | ①② | 2747 | 92 |
| 中午放学11:20~11:50 | ③④ | 1449 | 48 |
| 下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
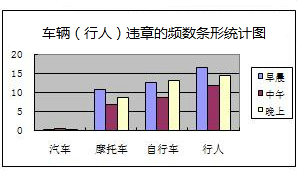 回答下列问题:
回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com