
分析 (1)分别表示出工作效率,根据工作时间乘以工作效率等于工作量列出方程求解即可;
(2)可以分三种情况来考虑,(1)班先做,然后两班合作,②(2)班先做,然后两班合作;③两班合作,分别列出方程,求解即可.
解答 解:(1)由题意得,(1)班的工作效率为:$\frac{1}{7.5}$=$\frac{2}{15}$,(2)班的工作效率为:$\frac{1}{6}$,
设还需合作x小时完成,
根据题意得:$\frac{2}{15}$×2+($\frac{2}{15}$+$\frac{1}{6}$)x=1,
解得:x=$\frac{22}{9}$,
所以前后共需$\frac{22}{9}$+2=$\frac{40}{9}$小时;
(2)①设(1)班先独做x小时,然后两班合做(4-x)小时,
由题意得:$\frac{2}{15}$x+($\frac{2}{15}$+$\frac{1}{6}$)(4-x)=1,
解得:x=1.2,
则4-1.2=2.8小时;
即先让(1)班做1.2小时,然后两班合做2.8小时;
②设(2)班先独做x小时,然后两班合做(4-x)小时,
由题意得:$\frac{1}{6}$x+($\frac{2}{15}$+$\frac{1}{6}$)(4-x)=1,
解得:x=1.5,
则4-1.5=2.5小时,
即先让(2)班做1.5小时,然后两班合做2.5小时;
③设两班合作x小时,
则($\frac{2}{15}$+$\frac{1}{6}$)x=1,
解得:x=$\frac{10}{3}$.
答:两班合作$\frac{10}{3}$小时.
点评 本题考查了一元一次方程的应用,要在规定时间内完成工作量,安排方法不止一种,同学们可以自己探讨.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
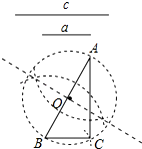 数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:
数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:| A. | 勾股定理 | B. | 直径所对的圆周角是直角 | ||
| C. | 勾股定理的逆定理 | D. | 90°的圆周角所对的弦是直径 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com