
【题目】在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在边AD上,且DF=BE,连接DE,CF.
(1)求证:四边形AECF是矩形;
(2)若DE平分∠ADC,AB=5,AD=8,求tan∠ADE的值.

【答案】(1)见解析;(2)![]()
【解析】
(1)证四边形AECF是平行四边形,再证出∠AEC=90°,即可得出结论;
(2)证出∠DEC=∠CDE,得出CD=CE=5,则BE=BC-CE=3,由勾股定理求出AE=4,再由三角函数定义即可得出答案.
解:(1)∵在平行四边形ABCD中
∴AD=BC,AD∥BC,
又∵DF=BE,
∴AF=EC
∴四边形AECF为平行四边形
∵∠AEC=90°
∴平行四边形AECF为矩形
(2)∵DE平分∠ADC,
∴∠ADE=∠CDE
∵AD∥BC
∴∠ADE=∠CED
∴∠CDE=∠CED
∴EC=DC=AB=5
∴BE=3
在Rt△ABE中,AE=![]() =4
=4
∵在矩形 AECF中
∴∠DAE=90°
∴tan∠ADE=![]() =
=![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】经过多方努力,北京市2019年在区域空气质量同步改善、气象条件较常年整体有利的情况下,大气环境中细颗粒物(![]() )等四项主要污染物同比均明显改善对北京市空气质量的有关数据进行收集、整理、描述与分析,下面给出了部分信息:
)等四项主要污染物同比均明显改善对北京市空气质量的有关数据进行收集、整理、描述与分析,下面给出了部分信息:
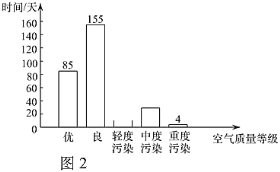
a.北京市2019年空气质量各级别分布情况如下图(全年无严重污染日)(不完整):

b.北京市2019年大气环境中二氧化硫(![]() )的年均浓度为4微克/立方米,稳定达到国家二级标准(60微克/立方米);
)的年均浓度为4微克/立方米,稳定达到国家二级标准(60微克/立方米);![]() ,二氧化氮(
,二氧化氮(![]() )的年均浓度分别为68微克/立方米,37微克/立方米,均首次达到国家二级标准(70微克/立方米,40微克/立方米);
)的年均浓度分别为68微克/立方米,37微克/立方米,均首次达到国家二级标准(70微克/立方米,40微克/立方米);![]() 的年均浓度为
的年均浓度为![]() 微克立方米,仍是北京市大气主要污染物,超过国家二级标准(35微克/立方米)的20%.
微克立方米,仍是北京市大气主要污染物,超过国家二级标准(35微克/立方米)的20%.
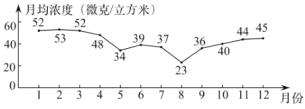
c.北京市2019年大气环境中![]() 月均浓度变化情况如下:
月均浓度变化情况如下:
二氧化硫(![]() )月均浓度(单位:微克/立方米)如下(不完整):
)月均浓度(单位:微克/立方米)如下(不完整):
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
月均浓度 | 9 | 6 | 5 | 4 | 3 | 2 | 3 | 3 | 5 | 4 |
(以上数据来源于北京市生态环境局官方网站)
根据以上信,回答下列问题:
(1)北京市2019年空气质量为“轻度污染”天数为( ).
A.82 B.92 C.102
(2)![]() 的值是______;
的值是______;
(3)北京市2019年大气环境中![]() 月均浓度达到国家二级标准的概率为______;
月均浓度达到国家二级标准的概率为______;
(4)北京市2019年大气环境中![]() 月均浓度的众数是4,则中位数是______.
月均浓度的众数是4,则中位数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为贯彻落实“绿水青山就是金山银山“的发展理念,投资组建了日废水处理量为m吨的废水处理车间,对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大,该车间经常无法完成当天工业废水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水,每天需固定成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.
(1)求该车间的日废水处理量m;
(2)为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过10元/吨,试计算该厂一天产生的工业废水量的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB垂直于弦CD,垂足为H,点P是弧AC上的一点(点P不与A,C重合),连结PC,PD,PA,AD,点E在AP的延长线上,PD与AB交于点F.给出下列四个结论:①CH2=AH·BH;②弧AD=弧AC;③AD2=DF·DP;④∠EPC=∠APD.
其中正确的个数有

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年的新冠肺炎病毒侵袭武汉时,全中国第一时间组织对武汉的救援.这其中,我国自主研制的大型运输机“运20”,为在疫情初期向武汉快速转运大量物资和人员作出了重要贡献.“运20”起飞重量220吨,从立项到成功编入部队,经历了20多年,仅研究初期的预研经费就超过3 000 000 000元人民币.将3 000 000 000用科学记数法表示为( )
A.3×108B.0.3×1010C.3×109D.30×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于点A和点B(点A在点B左侧),
与x轴交于点A和点B(点A在点B左侧),
(1)若抛物线的对称轴是直线x=1,求出点A和点B的坐标,并画出此时函数的图象;
(2)当已知点P(m,2),Q(-m,2m-1).若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)不透明的袋子A中装有红球1个、白球1个,不透明的袋子B中装有红球1个、白球2个,这些球除颜色外无其他差别.分别从两个袋子中随机摸出一个球,求摸出的两个球颜色不同的概率;
(2)甲、乙两人解同一道数学题,甲正确的概率为![]() ,乙正确的概率为
,乙正确的概率为![]() ,则甲乙恰有一人正确的概率是 .
,则甲乙恰有一人正确的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线:![]() ,与
,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() :
:![]() ,经过点
,经过点![]() ,且与
,且与![]() 轴的另一个交点为点
轴的另一个交点为点![]() .
.

(1)若![]() ,求此时抛物线的解析式、顶点坐标及点
,求此时抛物线的解析式、顶点坐标及点![]() 坐标;
坐标;
(2)在直线![]() 与抛物线
与抛物线![]() 围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
(3)①直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标会变吗?说明理由;
的坐标会变吗?说明理由;
②若抛物线![]() 与直线
与直线![]() 在
在![]() 的范围内有唯一公共点,请直接写出
的范围内有唯一公共点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com