
����Ŀ���ڿ��������У���ž�սʿ�ij���ۼ����ͣ��ض�������ĺ������������糿��![]() �س��������ϵ���
�س��������ϵ���![]() �أ�Լ����Ϊ��������ĺ���·�̼�¼���£���λ��ǧ�ף���
�أ�Լ����Ϊ��������ĺ���·�̼�¼���£���λ��ǧ�ף��� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
��![]() �������æȷ��
�������æȷ��![]() ��λ��
��λ��![]() �ص�ʲô������
�ص�ʲô������![]() �ض���ǧ�ף�
�ض���ǧ�ף�
��![]() �����ֹ����У�������������
�����ֹ����У�������������![]() ��Զ���ж�Զ������ֱ��д���𰸣�
��Զ���ж�Զ������ֱ��д���𰸣�
��![]() ���������ÿǧ����
���������ÿǧ����![]() ������������Ϊ
������������Ϊ![]() ���������۵�����ֹ��������ٻ��貹��������ͣ�
���������۵�����ֹ��������ٻ��貹��������ͣ�
���𰸡���![]() ��
��![]() ����
����![]() �صĶ���
�صĶ���![]() ǧ�ף�
ǧ�ף�
��![]() ������
������![]() ��Զ��
��Զ��![]() ǧ�ף�
ǧ�ף�
��![]() �����貹�������Ϊ9����
�����貹�������Ϊ9����
�������������������1������Ŀ��������ֵ��ӣ������Ϊ������B����A�صĶ����������Ϊ��������B����A�ص�������
��2���ֱ����������������ľ��룬ȡ��ֵ�ϴ�ĵ㼴�ɣ�
��3���������һ���ߵ���·�̣��ټ����һ��������������ȥ���������������;�л��貹���������
�����������1����14��9+8��7+13��6+12��5=20��
��B����A�صĶ���20ǧ�ף�
��2����·�̼�¼�и����������ľ���ֱ�Ϊ��
14ǧ�ף�14��9=5ǧ�ף�
14��9+8=13ǧ�ף�
14��9+8��7=6ǧ�ף�
14��9+8��7+13=19ǧ�ף�
14��9+8��7+13��6=13ǧ�ף�
14��9+8��7+13��6+12=25ǧ�ף�
14��9+8��7+13��6+12��5=20ǧ�ף�
����Զ���������25ǧ�ף�
��3����һ���ߵ���·��Ϊ��14+|��9|+8+|��7|+13+|��6|+12|+|��5|=74ǧ�ף�
Ӧ����74��0.5=37��������
�ʻ��貹�������Ϊ��37��28=9������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬����C��ֱ��m��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��m�ڵ�E������Ϊ��F������CD��BE��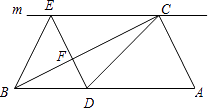
��1����֤��CE=AD��
��2������D��AB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
��3������A�Ĵ�С����ʲô����ʱ���ı���BECD�������Σ�������Ҫ֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧ��ȤС��8��ͬѧ�ı�ҵ��ѧ�������Գɼ�����Ϊ��30��29��28��27��28��29��30��28���������ݵ������ǣ�������
A. 27 B. 28 C. 29 D. 30
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������һö�ʵؾ��ȵ����ӣ�����������ֱ����1��6�ĵ����������¼�Ϊ��Ȼ�¼����ǣ�������
A.��������һ��ĵ���Ϊż��B.��������һ��ĵ���Ϊ3
C.��������һ��ĵ���С��7D.��������һ��ĵ���Ϊ6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�����ԲԲ���Ǹ������Σ��������Ľ��㣮
A.�����ߴ�ֱƽ����B.��������
C.������ƽ����D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ��ǣ���3��0������0��6��������P�ӵ�O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�����CP��COΪ�ڱ߹���PCOD�����߶�OP�ӳ�����ȡ��E��ʹPE=AO�����P�˶���ʱ��Ϊt�룮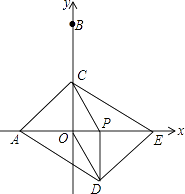
��1������C�˶����߶�OB���е�ʱ����t��ֵ����E�����ꣻ
��2������C���߶�OB��ʱ����֤���ı���ADECΪƽ���ı��Σ�
��3�����߶�PE��ȡ��F��ʹPF=2������F��MN��PE����ȡFM= ![]() ��FN=1���ҵ�M��N�ֱ��ڵ�һ�������ޣ����˶������У�����M��N�У���һ�������ı���ADEC�ı���ʱ��ֱ��д����������������t��ֵ��
��FN=1���ҵ�M��N�ֱ��ڵ�һ�������ޣ����˶������У�����M��N�У���һ�������ı���ADEC�ı���ʱ��ֱ��д����������������t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�У�AB��CD����BCD=90o��AB=AD=10cm��BC=8cm����P�ӵ�A������������ABCD������3cm/s���ٶ������˶�����Q�ӵ�D���������߶�
DC������2cm/s���ٶ������˶�. ��֪����ͬʱ��������һ���㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊt��s��.
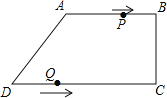
��1����CD�ij���
��2�����ı���PBQDΪƽ���ı���ʱ�����ı���PBQD���ܳ���
��3���ڵ�P��Q���˶������У��Ƿ����ijһʱ�̣�ʹ�á�BPQ�����Ϊ20cm2�������ڣ��������������������t��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com