
阅读下面材料:
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.
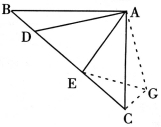
小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.

(1)∠B+∠D=180°(或互补);(2)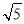 .
.
【解析】
试题分析:(1)如图,△ABE绕着点A逆时针旋转90°得到△ADG,利用全等的知识可知,要使EF=BE+DF,即EF=DG+DF,即要F、D、G三点共线,即∠ADG+∠ADF=180°,即∠B+∠D=180°.
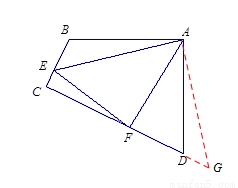
(2) 把△ABD绕A点逆时针旋转90°至△ACG,可使AB与AC重合,通过证明△AEG≌△AED得到DE=EG,由勾股定理即可求得DE的长.
(1)∠B+∠D=180°(或互补).
(2)∵ AB=AC,
∴ 把△ABD绕A点逆时针旋转90°至△ACG,可使AB与AC重合.
则∠B=∠ACG,BD=CG,AD=AG.
∵在△ABC中,∠BAC=90°,
∴∠ACB+∠ACG=∠ACB+∠B=90°于,即∠ECG=90°.
∴ EC2+CG2=EG2.
在△AEG与△AED中,
∠EAG=∠EAC+∠CAG=∠EAC+∠BAD=90°-∠EAD=45°=∠EAD.
又∵AD=AG,AE=AE,
∴△AEG≌△AED .
∴DE=EG.
又∵CG=BD,
∴ BD2+EC2=DE2.
∴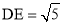 .
.
考点:1.面动旋转问题;2.全等三角形的判定和性质;3.勾股定理.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题
某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.求原计划每天生产多少台机器.
查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:选择题
西部大开发战略是党中央面向21世纪的重大决策,我国西部地区面积为6 400 000平方千米,将6 400 000用科学记数法表示应为( )
A. B.
B. C.
C.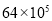 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:选择题
我国第六次全国人口普查数据显示,居住在城镇的人口总数达到666000000人.将666000000用科学记数法表示为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:利润=售价-进价)若商店计划销售完这批商品后能使利润达到1100元,问甲、乙两种商品应分别购进多少件?
| 甲 | 乙 |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:填空题
现定义运算“★”,对于任意实数a、b,都有a★b=a2﹣3a+b,如:3★5=32﹣3×3+5,根据定义的运算求2★(-1)= .若 x★2=6,则实数x的值是 .
查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:选择题
一元二次方程(x﹣2)=x(x﹣2)的解是( )
A.x=1 B.x=0 C.x1=2,x2=0 D.x1=2,x2=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com