练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    分解因式： .

     

    .

    【解析】

    试题分析：要将一个多项式分解因式的一般步骤是首先看各项有没有公因式，若有公因式，则把它提取出来，之后再观察是否是完全平方公式或平方差公式，若是就考虑用公式法继续分解因式．因此，

    先提取公因式a后继续应用完全平方公式分解即可：.

    考点：提公因式法和应用公式法因式分解.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014年北京市房山区中考一模数学试卷（解析版） 题型：选择题

    如图，直线m∥n，将含有45°角的三角板ABC的直角顶点C放在直线n上，则∠1+∠2等于（ ）

    A．30° B．40° C．45° D．60°

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市平谷区中考一模数学试卷（解析版） 题型：解答题

    如图，点A、C、D、B四点共线，且AC=DB，∠A=∠B，∠E=∠F．求证：DE=CF．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市密云县中考一模数学试卷（解析版） 题型：解答题

    如图，在Rt△ABC中，∠ACB=90°，点D是AB边上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．

    （1）求证：BD=BF；

    （2）若CF=1，cosB=，求⊙O的半径．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市密云县中考一模数学试卷（解析版） 题型：解答题

    已知：如图，点A，D，C在同一直线上，AB∥EC，AC=CE，∠B=∠EDC

    求证：BC=DE

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市密云县中考一模数学试卷（解析版） 题型：选择题

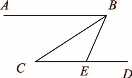
    如图，已知AB∥CD，BC平分∠ABE，∠C=，则∠BED 的度数是（ ）

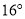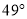    A. B． C． D．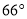

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市东城区中考一模数学试卷（解析版） 题型：解答题

    阅读下面材料：

    小炎遇到这样一个问题：如图1，点E、F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连结EF，则EF=BE+DF，试说明理由．

    小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中．她先后尝试了翻折、旋转、平移的方法，最后发现线段AB，AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决了这个问题（如图2）．

    参考小炎同学思考问题的方法，解决下列问题：

    （1）如图3，四边形ABCD中，AB=AD，∠BAD=90°点E，F分别在边BC，CD上，∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足_ 关系时，仍有EF=BE+DF；

    （2）如图4，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°，若BD=1， EC=2，求DE的长．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市东城区中考一模数学试卷（解析版） 题型：选择题

    在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同．其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（ ）

    A．众数 B．方差 C．平均数 D．中位数

     

    查看答案和解析>>

    科目：初中数学 来源：2014届山东省泰安市泰山区初三下学期期末数学试卷（解析版） 题型：填空题

    如图，在四边形ABCD中，对角线AC、BD交于点O，AD∥BC，请添加一个条件：　_________　，使四边形ABCD为平行四边形（不添加任何辅助线）．

     

     

    查看答案和解析>>

    同步练习册答案