
如图,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F.
(1)求证:BD=BF;
(2)若CF=1,cosB= ,求⊙O的半径.
,求⊙O的半径.

(1)证明见解析;(2) .
.
【解析】
试题分析:(1)由平行线的性质、等腰三角形的性质推知∠OED=∠F,则易证得结论.
(2)由cosB= ,设BC=3x,AB=5x,根据OE∥BF,得∠AOE=∠B,从而
,设BC=3x,AB=5x,根据OE∥BF,得∠AOE=∠B,从而 .因此列出关于半径r的方程,通过解方程即可求得r的值,进而得到⊙O的半径.
.因此列出关于半径r的方程,通过解方程即可求得r的值,进而得到⊙O的半径.
(1)如图,连接OE,
∵AC与⊙O相切于点E,
∴OE⊥AC,即∠OEC=900.
∵∠ACB=900,∴∠OEC=∠ACB.∴OE∥BC.
∴∠OED=∠F.
∵OE=OD,∴∠OED=∠ODE.∴∠F=∠ODE.
∴BD=BF.

(2)∵cosB= ,∴设BC=3x,AB=5x.
,∴设BC=3x,AB=5x.
∵CF=1,∴ .
.
由(1)知,BD=BF,∴ .∴
.∴ .
.
∴ ,
, .
.
∵OE∥BF,∴∠AOE=∠B。∴ ,即
,即 ,解得
,解得 ,
, .
.
∴⊙O的半径为 .
.
考点:1.切线的性质;2.平行的判定和性质;3.等腰三角形的判定和性质;4.锐角三角函数定义.


科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:解答题
在平面直角坐标系中,已知抛物线 (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限.
(1)如图,若该抛物线过A,B两点,求b,c的值;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与直线AC交于另一点Q.
①点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M,P,Q三点为顶点的三角形是以PQ为腰的等腰直角三角形时,求点M的坐标;
②取BC的中点N,连接NP,BQ.当 取最大值时,点Q的坐标为________.
取最大值时,点Q的坐标为________.

查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:选择题
如图,在矩形ABCD中,AB=9,BC=3,点E是沿A→B方向运动,点F是沿A→D→C方向运动.现E、F两点同时出发匀速运动,设点E的运动速度为每秒1个单位长度,点F的运动速度为每秒3个单位长度,当点F运动到C点时,点E立即停止运动.连接EF,设点E的运动时间为x秒,EF的长度为y个单位长度,则下列图象中,能表示y与x的函数关系的图象大致是 ( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:选择题
西部大开发战略是党中央面向21世纪的重大决策,我国西部地区面积为6 400 000平方千米,将6 400 000用科学记数法表示应为( )
A. B.
B. C.
C.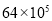 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:利润=售价-进价)若商店计划销售完这批商品后能使利润达到1100元,问甲、乙两种商品应分别购进多少件?
| 甲 | 乙 |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
查看答案和解析>>
科目:初中数学 来源:2014届重庆一中七年级上期期末考试数学试卷(解析版) 题型:选择题
“十二五”期间,我国将新建保障性住房36 000 000套,用于解决中低收入人群和新参加工作的大学生住房的需求,将36 000 000用科学记数法表示应是 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com