
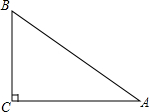
 如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用?
如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用? 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
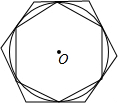 如图,正六边形T1的6个顶点都在⊙O上,正六边形T2的6条边都和⊙O相切(我们称T1、T2分别为⊙O的内接正六边形和外切正六边形)
如图,正六边形T1的6个顶点都在⊙O上,正六边形T2的6条边都和⊙O相切(我们称T1、T2分别为⊙O的内接正六边形和外切正六边形)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com