
【题目】如图,四边形ABCD是正方形,E,F分别在线段BC和CD上,![]() .连接EF。将△ADF绕着点顺时针旋转90°,得到
.连接EF。将△ADF绕着点顺时针旋转90°,得到![]()
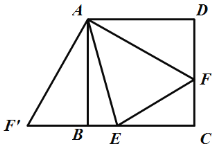
(1)证明:![]()
(2)证明:EF=BE+DF.
(3)已知正方形ABCD边长是6,EF=5,求线段BE的长.
【答案】(1)见解析;(2)见解析(3)2或3
【解析】
(1)由旋转的性质得到![]() ,
,![]() ,
,![]() ,然后得到
,然后得到![]() ,利用SAS证明三角形全等即可;
,利用SAS证明三角形全等即可;
(2)由(1)知DF=BF’,即可得到EF=BE+DF;
(3)设BE=x,则DF=5-x,得到CF=x+1,利用勾股定理得![]() ,即可求出BE的长度.
,即可求出BE的长度.
解:(1)由旋转的性质可得![]() ,
,![]() ,
,![]() 。
。
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴EF=BE+DF;
(3)∵BE=x,EF=BE+DF ,EF=5,
∴DF=5-x,
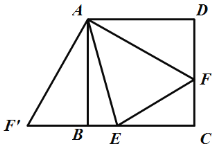
又∵正方形ABCD边长是6,即BC=CD=6,
∴CE=BC-BE=6-x,CF=CD-DF=6-(5-x)=x+1,
在Rt△CEF中,有![]() ,
,
即![]() ,
,
解得:![]() ;
;
∴线段BE的长为2或3.


科目:初中数学 来源: 题型:
【题目】如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.
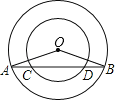
(1)求证AC=BD;
(2)若AC=3,大圆和小圆的半径分别为6和4,则CD的长度是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
| 0 | 2 | 3 | 4 |
| 5 | 0 |
|
| 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④3是方程
;④3是方程![]() 的一个根;⑤若
的一个根;⑤若![]() ,
,![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() ,它与
,它与![]() 轴交于
轴交于![]() 、
、![]() ,且
,且![]() 、
、![]() 位于原点两侧,与
位于原点两侧,与![]() 的正半轴交于
的正半轴交于![]() ,顶点
,顶点![]() 在
在![]() 轴右侧的直线
轴右侧的直线![]() :
:![]() 上,则下列说法:①
上,则下列说法:①![]() ②
②![]() ③
③![]() ④
④![]() 其中正确的结论有( )
其中正确的结论有( )
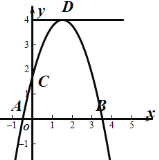
A.①②B.②③C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
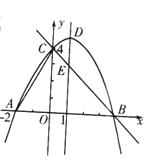
【题目】如图,抛物线![]() 与
与![]() 轴交于点C(O,4),与
轴交于点C(O,4),与![]() 轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴
轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴![]() 与抛物线交于点D,与直线BC交于点E.
与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线Z与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
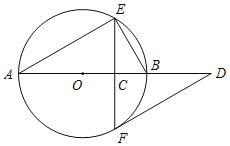
【题目】如图,AB是⊙O的直径,弦EF⊥AB于点C,过点F作⊙O的切线交AB的延长线于点D.
(1)已知∠A=α,求∠D的大小(用含α的式子表示);
(2)取BE的中点M,连接MF,请补全图形;若∠A=30°,MF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地,颜色等其他方面完全相同,若背面上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面向上放在桌面上,从中先随机抽取一张卡片,记该卡片上的数字为x,再把剩下的两张卡片洗匀后,背面向上放在桌面上,再从这两张卡片中随机抽取一张卡片,记该卡片上的数字为y.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,写出(x,y)所有可能出现的结果.
(2)求取出的两张卡片上的数字之和为偶数的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一动点,
上一动点,![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处;延长
处;延长![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() .
.
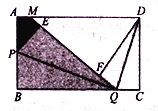
(1)求证:![]() ≌
≌![]() ;
;
(2)当![]() 时,将
时,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在线段
落在线段![]() 上点
上点![]() 处.
处.
①求证:![]() ∽
∽![]() ;
;
②如果![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com