
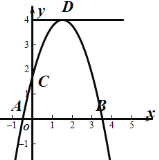
【题目】如图,已知二次函数![]() ,它与
,它与![]() 轴交于
轴交于![]() 、
、![]() ,且
,且![]() 、
、![]() 位于原点两侧,与
位于原点两侧,与![]() 的正半轴交于
的正半轴交于![]() ,顶点
,顶点![]() 在
在![]() 轴右侧的直线
轴右侧的直线![]() :
:![]() 上,则下列说法:①
上,则下列说法:①![]() ②
②![]() ③
③![]() ④
④![]() 其中正确的结论有( )
其中正确的结论有( )
A.①②B.②③C.②③④D.①②③④
【答案】C
【解析】
先由抛物线解析式得到a=-1<0,利用抛物线的对称轴得到b>0,易得c>0,于是可对①进行判断;由顶点D在y轴右侧的直线l:y=4上可得b的范围,从而可判断②是否正确;由a=-1及顶点D在y轴右侧的直线l:y=4上,可得抛物线与x轴两交点之间的距离AB为定值,即可求得AB的长度及S△ABD的大小.
解: ∵A,B两点位于y轴两侧,且对称轴在y轴的右侧,
∴![]() ,
,
∵![]() ,
,
则b>0,
函数图像交y轴于C点,则c>0,
∴bc>0,即①错误;
又∵顶点坐标为(![]() ),即(
),即(![]() )
)
∴![]() =4,即
=4,即![]()
又∵![]() =
=![]() ,即
,即![]()
∴AB=4即③正确;
又∵A,B两点位于y轴两侧,且对称轴在y轴的右侧
∴![]() <2,即b<4
<2,即b<4
∴0<b<4,故②正确;
∵顶点的纵坐标为4,即△ABD的高为4
∴△ABD的面积=![]() ,故④正确;
,故④正确;
故答案为:C.


科目:初中数学 来源: 题型:
【题目】已知矩形![]() 中,
中,![]() ,动点
,动点![]() 从
从![]() 点出发,以2cm/s的速度沿
点出发,以2cm/s的速度沿![]() 向终点
向终点![]() 匀速运动,连接
匀速运动,连接![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() s .
s .
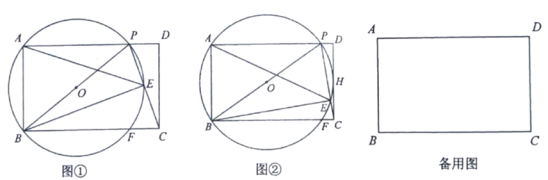
(1)如图①,若点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
(2)如图②,若⊙![]() 与
与![]() 相切于点
相切于点![]() ,求
,求![]() 的值;
的值;
(3)若![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
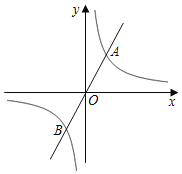
【题目】直线y=mx(m为常数)与双曲线y=![]() (k为常数)相交于A、B两点.
(k为常数)相交于A、B两点.
(1)若点A的横坐标为3,点B的纵坐标为﹣4.直接写出:k= ,m= ,mx>![]() 的解集为 .
的解集为 .
(2)若双曲线y=![]() (k为常数)的图象上有点C(x1,y1),D(x2,y2),当x1<x2时,比较y1与y2的大小.
(k为常数)的图象上有点C(x1,y1),D(x2,y2),当x1<x2时,比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点![]() 的正前方
的正前方![]() 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为![]() 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为![]() .已知球门的横梁高
.已知球门的横梁高![]() 为
为![]() .
.

![]() 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
![]() 守门员乙站在距离球门
守门员乙站在距离球门![]() 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为![]() ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一位篮球运动员在距离篮圈中心水平距离![]() 处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为
处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为![]() 时,达到最大高度
时,达到最大高度![]() ,然后准确落入篮筐内,已知篮圈中心距离地面高度为
,然后准确落入篮筐内,已知篮圈中心距离地面高度为![]() ,试解答下列问题:
,试解答下列问题:
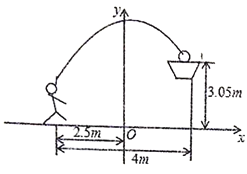
(1)建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式.
(2)这次跳投时,球出手处离地面多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E,F分别在线段BC和CD上,![]() .连接EF。将△ADF绕着点顺时针旋转90°,得到
.连接EF。将△ADF绕着点顺时针旋转90°,得到![]()
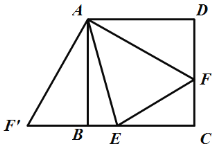
(1)证明:![]()
(2)证明:EF=BE+DF.
(3)已知正方形ABCD边长是6,EF=5,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:
如图,
(1)连接OP,作线段OP的垂直平分线MN交OP于点C;
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点;
(3)作直线PA,PB.所以直线PA,PB就是所求作的切线.
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是_____;由此可证明直线PA,PB都是⊙O的切线,其依据是_____.
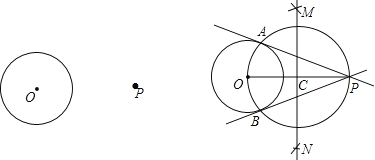
查看答案和解析>>
科目:初中数学 来源: 题型:
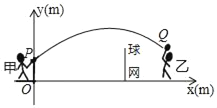
【题目】甲、乙两人进行羽毛球比赛,把球看成点,其飞行的路线为抛物线的一部分.如图建立平面直角坐标系,甲在O点正上方1m的P处发球,羽毛球飞行的高度y(m)与羽毛球距离甲站立位置(点O)的水平距离x(m)之间满足函败表达式y=a(x﹣4)2+h.已知点O与球网的水平距离为5m,球网的高度为1.55m,球场边界距点O的水平距离为10m.
(1)当a=﹣![]() 时,求h的值,并通过计算判断此球能否过网.
时,求h的值,并通过计算判断此球能否过网.
(2)若甲发球过网后,乙在另一侧距球网水平距离lm处起跳扣球没有成功,球在距球网水平距离lm,离地面高度2.2m处飞过,通过计算判断此球会不会出界?
查看答案和解析>>
科目:初中数学 来源: 题型:
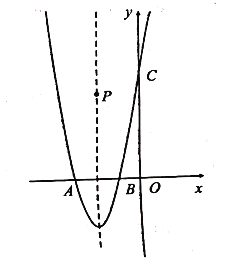
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(2)我们规定:对于直线![]() ,直线
,直线![]() ,若
,若![]() ,则直线
,则直线![]() ;反过来也成立.请根据这个规定解决下列问题:
;反过来也成立.请根据这个规定解决下列问题:
①直线![]() 与直线
与直线![]() 是否垂直?并说明理由;
是否垂直?并说明理由;
②若点![]() 是抛物线
是抛物线![]() 的对称轴上一动点,是否存在点
的对称轴上一动点,是否存在点![]() 与点
与点![]() ,点
,点![]() 构成以
构成以![]() 为直角边的直角三角形?若存在,请求出点
为直角边的直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com