
如图1,在平面直角坐标系中,抛物线 (
( )经过点
)经过点 ,顶点为
,顶点为 .
.

(1)求抛物线 的解析式;
的解析式;
(2)如图2,先将抛物线 向上平移使其顶点在原点
向上平移使其顶点在原点 ,再将其顶点沿直线
,再将其顶点沿直线 平移得到抛物线
平移得到抛物线 ,设抛物线
,设抛物线 与直线
与直线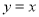 交于
交于 、
、 两点,求线段
两点,求线段 的长.
的长.
(3)在图1中将抛物线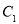 绕点
绕点 旋转
旋转 后得到抛物线
后得到抛物线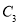 ,直线
,直线 总经过一个定点
总经过一个定点 ,若过定点
,若过定点 的直线
的直线 与抛物线
与抛物线 只有一个公共点,求直线
只有一个公共点,求直线 的解析式.
的解析式.
(1)y=x2-1;(2)CD= ;(3)过定点M,共有三条直线l: x=2 或y=
;(3)过定点M,共有三条直线l: x=2 或y= x+4
x+4 或y=
或y= x+4+
x+4+ ,它们分别与抛物线C3只有一个公共点
,它们分别与抛物线C3只有一个公共点
【解析】
试题分析:(1)y=x2-1
(2)可设抛物线C2的顶点为(m, m),
依题意抛物线C2 为 ,
,
与直线y=x联立解方程组得:x1=m,y1=m; x2=m+,1,y2=m+1.
即C(m, m), D(m+1, m+1 )
过点C作CH∥x轴,过点D作DN∥y轴,CH交DN于点M,
∴CM=1,DM=1, ∴CD= .
.
(3)依题意可求出抛物线C3的解析式为 +1
+1
直线 =k(x-2)+4, ∴定点M为(2, 4)
=k(x-2)+4, ∴定点M为(2, 4)
①经过定点M,与y轴平行的直线l:x=2与抛物线C3总有一个公共点(2,1).
②经过定点M的直线l为一次函数 (k≠0)的图象,
(k≠0)的图象,
与 +1联立方程组,消去y得x2-4x+3+kx-2k+4=0
+1联立方程组,消去y得x2-4x+3+kx-2k+4=0
即x2-(4-k)x+7 -2k=0, △=k2-12=0,得k1= , k2=
, k2=
∴y= x+4
x+4 或y=
或y= x+4+
x+4+
综上所述,过定点M,共有三条直线l: x=2 或y= x+4
x+4 或y=
或y= x+4+
x+4+ ,它们分别与抛物线C3只有一个公共点.
,它们分别与抛物线C3只有一个公共点.
考点: 抛物线的综合运用


科目:初中数学 来源:2014-2015学年湖北省宜城市九年级上学期期中考试数学试卷(解析版) 题型:选择题
对于二次函数 的图象,下列说法正确的是( )
的图象,下列说法正确的是( )
A.开口向上
B.对称轴是
C.顶点坐标是(-1,3)
D.与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜城市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,平行于x轴的直线AC分别交抛物线 (x≥0)与
(x≥0)与 (x≥0)于B、C两点,过点C作y轴的平行线交
(x≥0)于B、C两点,过点C作y轴的平行线交 于点D,直线DE∥AC,交
于点D,直线DE∥AC,交 于点E,则
于点E,则 = _______.
= _______.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省八年级上学期第一次月考数学卷(解析版) 题型:选择题
如图,已知AF平分∠BAC,过F作FD⊥BC,若∠B比∠C大20度,则∠F的度数是( )
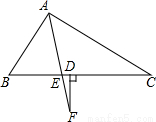
A.10度 B.15度 C.20度 D.不能确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级12月联考数学试卷(解析版) 题型:解答题
袋中装有大小相同的2个红球和2个绿球(1) 先从袋中摸出1个球后放回,混合均匀后再摸出1个球.① 求第一次摸到绿球,第二次摸到红球的概率 (请直接写出结果)② 求两次摸到的球中有1个绿球和1个红球的概率
(请直接写出结果)② 求两次摸到的球中有1个绿球和1个红球的概率 (请直接写出结果)(2) 先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率
(请直接写出结果)(2) 先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率 是多少?(请用画出树形图或列表法求出结果)
是多少?(请用画出树形图或列表法求出结果)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级12月联考数学试卷(解析版) 题型:填空题
如图,已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是__________.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(8分)如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:

(1)以A点为旋转中心,将△ABC绕点A顺时针旋转 得△AB1C1,画出△AB1C1.
得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点 . 若点
. 若点 向右平移x(x取整数)个单位长度后落在△A2B2C2的内部,请直接写出x的值.
向右平移x(x取整数)个单位长度后落在△A2B2C2的内部,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省八年级上学期第一次月考数学卷(解析版) 题型:解答题
(9分)在△ABC中,∠A=400,高BE、CF交于点O,求∠BOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com