
【题目】某自行车厂计划一周生产自行车1400辆,由于种种原因,每天生产量不同.下表是某周的生产变化情况,上周日生产200辆(正数表示比前一天多生产的辆数,负数表示比前一天少生产的辆数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
辆数变化(单位:辆) |
|
|
|
|
|
|
|
(1)根据记录的数据可知该厂这周星期四生产了多少辆自行车?
(2)这周产量最多的一天比产量最少的一天多生产了多少辆自行车?
(3)根据记录的数据可知该厂本周实际生产了多少辆自行车?
(4)该厂实行每周计件工资制,每生产一辆车可得50元,若超额完成任务,则超过部分每辆另外奖励20元,少生产一辆扣25元,那么该厂工人这一周的工资总额是多少元?
【答案】(1)200;(2)12;(3) 1399;(4) 69975
【解析】
(1)根据上周日生产200辆,再结合题中表所示即可得出周四生产的自行车数量;
(2)根据表中所提供的信息,得出每一天的产量,再找出产量最多的一天和产量最少的一天即可得出结果;
(3)将题目(2)中每一天的产量求和即可得出结果;
(4)原计划一周生产自行车1400辆,实际一周生产了1399辆,结合题目已知条件即可得出结果.
解:(1)周四生产的自行车:200+6-7-1+2=200(辆)
(2)星期一自行车产量:200+6=206(辆);
星期二自行车产量:206-7=199(辆);
星期三自行车产量:199-1=198(辆);
星期四自行车产量:198+2=200(辆);
星期五自行车产量:200-3=197(辆);
星期六自行车产量:197+8=205(辆);
星期日自行车产量:205-11=194(辆).
产量最多的一天为是星期一,最少的一天为星期日;
故206-194=12(辆).
∴这周产量最多的一天比产量最少的一天多生产了12辆自行车.
(3)由题(2)知:206+199+198+200+197+205+194=1399(辆).
∴本周实际生产了1399辆自行车.
(4)由题(3)知:1400×50-25=69975(元).
∴该厂工人这一周的工资总额是69975元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】今年暑假,小丽爸爸的同事送给她爸爸一张北京故宫的门票,她和哥哥两人都很想去参观,可门票只有一张.读九年级的哥哥想了一个办法,他拿了八张扑克牌,将数字为1,2,3,5的四张牌给小丽,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小利哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌上的数字相加,如果和为偶数,和小丽去;如果和为奇数,则哥哥去.
(1)请用画树状图或列表的方法求小丽去北京故宫参观的概率;
(2)哥哥设计的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从某点![]() 点处出发在一直线上来回爬行,假定向右爬行的路程记为正数,左爬行的路程为负数,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-11.
点处出发在一直线上来回爬行,假定向右爬行的路程记为正数,左爬行的路程为负数,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-11.
(1)小虫最后是否回到出发点![]() 点?如果不在,请说出小虫的位置;
点?如果不在,请说出小虫的位置;
(2)小虫离开出发点![]() 点最远时是 厘米;
点最远时是 厘米;
(3)在爬行过程中,如果每爬1厘米奖励两粒芝麻,则小虫共得多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)阅读下列材料:
(1)关于x的方程x2-3x+1=0(x≠0)方程两边同时乘以![]() 得:
得: ![]() 即
即![]() ,
, ![]() ,
,
(2)a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)x2-4x+1=0(x≠0),则![]() = ______ ,
= ______ , ![]() = ______ ,
= ______ , ![]() = ______ ;
= ______ ;
(2)2x2-7x+2=0(x≠0),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
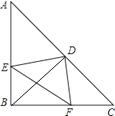
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边中点,过D点作DE⊥DF,交AB于E,交BC于F,连接BD.
(1)求证:△CDF≌△BED
(2)若AE=4,FC=3,求AB长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com