
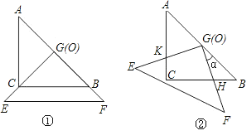
【题目】把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
(1)在上述旋转过程中,BH与CK有怎样的数量关系四边形CHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的![]() ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.
【答案】(1)、BH=CK;四边形CHGK的面积不变;证明过程见解析;(2)、y=![]()
![]() -2x+4(0<x<4);(3)、x=1或x=3.
-2x+4(0<x<4);(3)、x=1或x=3.
【解析】
试题(1)连接CG,根据中线的性质得出CG=BG,CG⊥AB,根据旋转图形的性质得出△BGH和△CGK全等,将四边形的面积转化成△CHG的面积+△CGK的面积,根据全等得出△CHG的面积+△BGH的面积,即△ABC面积的一半;(2)连接HK,则BK=CK=x,CH=4-x,根据△GHK的面积=四边形CHGK的面积-△CHK的面积求出函数关系式;(3)根据(2)中的结论列出一元二次方程,然后求出x的值.
试题解析:(1)在上述旋转过程中,BH=CK,四边形CHGK的面积不变。
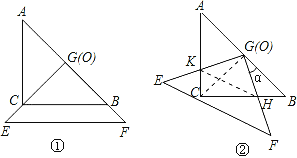
证明:连接CG,
∵△ABC为等腰直角三角形,O(G)为其斜边中点,∴CG=BG,CG⊥AB,
∴∠ACG=∠B=45°,∵∠BGH与∠CGK均为旋转角,∴∠BGH=∠CGK,
在△BGH与△CGK中,∠B=∠KCG,BG=CG, ∠BCG=∠CGK
∴△BGH≌△CGK(ASA), ∴BH=CK,△BGH的面积=△CGK的面积.
∴四边形CHGK的面积=△CHG的面积+△CGK的面积=的面积△CHG+△BGH的面积=![]() S△ABC=
S△ABC=![]() ×
×![]() ×4×4=4
×4×4=4
即:四边形CHGK的面积为4,是一个定值,在旋转过程中没有变化;
(2)∵AC=BC=4,BK=x,∴CH=4-x,CK=x,连接HK.
由△GHK的面积=四边形CHGK的面积-△CHK的面积,得y=4-![]() x(4-x)=
x(4-x)=![]()
![]() -2x+4 由0°<α<90°,得到BH最大=BC=4,∴0<x<4;
-2x+4 由0°<α<90°,得到BH最大=BC=4,∴0<x<4;
(3)存在.根据题意,得![]()
![]() -2x+4=
-2x+4=![]() ×8 解这个方程,得
×8 解这个方程,得![]() =1,
=1,![]() =3,
=3,
即:当x=1或x=3时,△GHK的面积均等于△ABC的面积的![]() 。
。


科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥CD,垂足为P,则∠EPF=

A.35°B.45°C.50°D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
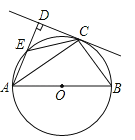
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
(1)求证:CE=CB;
(2)若AC=![]() ,CE=
,CE=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级学生足球训练情况,随机抽查该年级若干名学生进行测试,然后把测试结果分为4个等级:A、B、C、D,并将统计结果绘制成两幅不完整的统计图.请根据图中的信息解答下列问题:
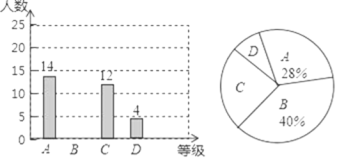
(1)在这次调查中,一共调查了 名学生,扇形统计图中,C等级对应的扇形圆心角是 °.
(2)补全条形统计图.
(3)该年级共有900人,估计该年级足球测试成绩为D等的人数为 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,则长方形卡片的周长为_____.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+bx+c经过点B(-1,0)和点C(2,3).
(1)求此抛物线的函数表达式;
(2)如果此抛物线上下平移后过点(-2,-1),请直接写出平移的方向和平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
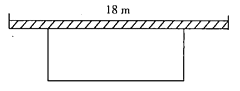
【题目】如图,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为18m),另外三边利用学,校现有总长38m的铁栏围成.
(1)若围成的面积为![]() ,试求出自行车车棚的长和宽;
,试求出自行车车棚的长和宽;
(2)能围成面积为![]() 的自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.
的自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com