
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 5 | 2 | 1 | 2 | 5 | … |


科目:初中数学 来源: 题型:
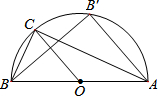 如图,△ABC内接于⊙O,∠ACB=90°,BC=a,AB=c(c>
如图,△ABC内接于⊙O,∠ACB=90°,BC=a,AB=c(c>| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是一个长方形建筑物,建筑物旁边的空地上长满青草,点M是AB的中点,AB=10米,在点M处系着一只羊,绳长为6米,
如图是一个长方形建筑物,建筑物旁边的空地上长满青草,点M是AB的中点,AB=10米,在点M处系着一只羊,绳长为6米,查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某家设计公司设计了这样一种纸扇:纸扇张开的最大角度θ与360°-θ的比为黄金比,那么制作一把这样的纸扇至少需要用多少平方厘米的纸?(纸扇有两面,结果精确到0.1cm2)
如图,某家设计公司设计了这样一种纸扇:纸扇张开的最大角度θ与360°-θ的比为黄金比,那么制作一把这样的纸扇至少需要用多少平方厘米的纸?(纸扇有两面,结果精确到0.1cm2)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com