Question

11．已知函数y=$\frac{1}{2}$x²，y=$\frac{1}{2}$（x+2）²+2和y=$\frac{1}{2}$（x+2）²-3
（1）在同一个平面直角坐标系中画出这三个函数的图象；
（2）分别说出这三个函数的图象的开口方向、对称轴和顶点坐标；
（3）试讨论函数y=$\frac{1}{2}$（x+2）²-3的性质．

Answer 1

分析 （1）建立平面直角坐标系，然后根据二次函数图象的作法画出图象即可．
（2）分别由图象可得出开口方向、对称轴及顶点坐标．
（3）可以从开口方向、对称轴、顶点坐标及增减性方面来谈．

解答 解：（1）y=$\frac{1}{2}$x²，y=$\frac{1}{2}$（x+2）²+2和y=$\frac{1}{2}$（x+2）²-3的图象如图所示：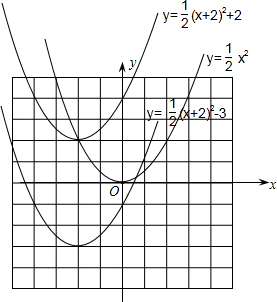

（2）函数y=$\frac{1}{2}$x²的图象开口向上，对称轴是y轴，顶点是（0，0）；
函数y=$\frac{1}{2}$（x+2）²+2的图象开口向上，对称轴是直线x=-2，顶点是（-2，2）；
函数y=$\frac{1}{2}$（x+2）²-3的图象开口向上，对称轴是直线x=-2，顶点是（-2，-3）；
（3）函数y=$\frac{1}{2}$（x+2）²-3的性质：
①开口方向向上；
②对称轴x=-2；
③顶点坐标（-2，-3）；
④当x＞-2时，函数y的值随x的增大而增大；当x＜-2时，函数y的值随x的增大而减小；当x=-2时，函数y取的最小值-3．

点评 本题考查了二次函数的图象和性质，解题的关键是能够正确的作出二次函数的图象，掌握函数的性质．