
����Ŀ��Ϊ�˽�ij��ѧѧ�����������������ϲ���������顢������������ӡ����ʵ���ĸ�������������е���ͳ�ƣ��ִӸ�У�����ȡn��ѧ����Ϊ�����������ʾ�����ķ�ʽ�ռ����ݣ������ʾ������ÿ��ѧ��ֻ��ѡ������һ�.�����ݵ���õ������ݻ��Ƴ�����ͼ��ʾ��������������ͳ��ͼ����ͼ���ṩ����Ϣ������������⣺
��1����ֱ�Ӳ�ȫ����ͳ��ͼ��
��2������У����ѧ��3200�����Թ��Ƹ�Уϲ�����������ѧ��������
��3����������ϲ���������4��ѧ������3��������1��Ů�����ִ���4��ѧ���������ȡ2���������б�����״ͼ�ķ�����ǡ�ó�2�������ĸ���.
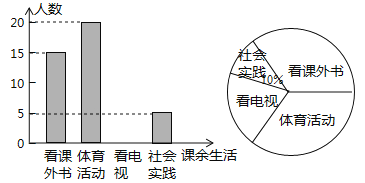
���𰸡���1�������ӵ�ѧ����10�ˣ�ͼ�ԣ�����2��Լ��960�˰��������飻��3������Ϊ![]() �����̼�������
�����̼�������
��������
1������ϲ�����ʵ����������������ռ�İٷֱȼ������������������ټ���������ӵ�������Ȼ��ȫ����ͳ��ͼ��
��2����3200����������ϲ���������������İٷֱȿɹ��Ƹ�Уϲ�����������ѧ������
��3������״ͼչʾ����12�ֵȿ��ܵĽ���������ҳ�ǡ�ó鵽2���еĽ������Ȼ����ݸ��ʹ�ʽ���㣮
�⣺��1�������������Ϊ5��10%=50���ˣ���
���Կ����ӵ�����Ϊ50-15-20-5=10���ˣ���
��ȫ����ͳ��ͼΪ��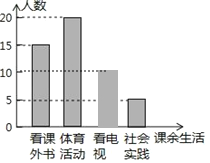
��2��3200��![]() =960��
=960��
���Թ��Ƹ�Уϲ�����������ѧ����Ϊ960�ˣ�
��3������״ͼ��
����12�ֵȿ��ܵĽ����������ǡ�ó鵽2���еĽ����Ϊ6��
����ǡ�ó鵽2���еĸ���=![]() =
=![]() ��
��


 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ�����O��AB=AC���ӳ�BC����D��ʹCD=CA������AD����O�ڵ�E������BE��CE��
��1����֤����ABE�ա�CDE��
��2����գ�
������ABC�Ķ���Ϊ�� ��ʱ���ı���AOCE�����Σ�
����AE=6��EF=4��DE�ij��� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���(x��2)(x��3)=m��ʵ����x1��x2����x1��x2��
(1)��m��ȡֵ��Χ��
(2)���������̵�����ʵ���ֱ�Ϊx1=����x2=����������������m��0ʱ���ԱȽ���������2��3�Ĵ�С�����á��������ӣ�
(3)����κ���y=(x��x1)(x��x2)��m��ͼ����x��Ľ������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У��Ե�AΪԲ�ģ�AB�ij�Ϊ�뾶��Բǡ����CD�����ڵ�C����AD�ڵ�E����BA���ӳ����ڵ�F������EF�ij�Ϊ������ͼ����Ӱ���ֵ����Ϊ______��
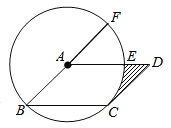
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��![]() ��x�ύ��A��C��A��C����ࣩ����B���������ϣ��������Ϊ1������BC��BO����FΪOB�е㣮
��x�ύ��A��C��A��C����ࣩ����B���������ϣ��������Ϊ1������BC��BO����FΪOB�е㣮

��1����ֱ��BC�ĺ�������ʽ��
��2������DΪ�����ߵ��������ϵ�һ�����㣬����BD��CD����EΪx����һ���㣬����BCD����������ʱ�����D�����꣬��|FE��DE|�����ֵ��
��3����ͼ2������G���B���������߶Գ���Գƣ�ֱ��BG��y�ύ�ڵ�M����N���߶�BG�ϵ�һ���㣬����NF��MF������NFO��3��BNFʱ������CN����ֱ��BO�Ƶ�O��ת������ת�е�ֱ��BOΪB��O��ֱ��B��O��ֱ��CN���ڵ�Q������OCQΪ����������ʱ�����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��PΪ����
��PΪ����![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() Ϊ����������
Ϊ����������![]() ��ʹ��F���߶�
��ʹ��F���߶�![]() ���ӳ����ϣ�����
���ӳ����ϣ�����![]() .
.
��1����ͼ1������P���߶�![]() ���ӳ����ϣ��ж�
���ӳ����ϣ��ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��2����ͼ2������P���߶�![]() ��
��
������P���߶�![]() ���е㣬�ж�
���е㣬�ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
�ڵ�![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() �Ķ���.
�Ķ���.
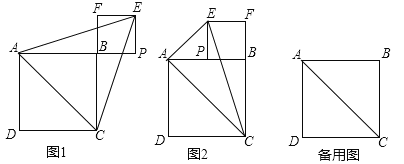
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ڵ���ֱ���������У�![]() ��
��![]() ��D��E�ֱ���
��D��E�ֱ���![]() �ϣ���
�ϣ���![]() ����ʱ��
����ʱ��![]() ��
��![]() ��
��
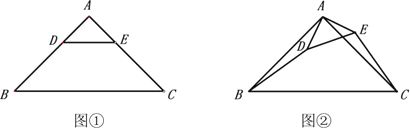
(1)��ͼ����![]() �Ƶ�A��ת����ͼ��ʱ���������Ƿ���Ȼ����������������֤����������������˵������.
�Ƶ�A��ת����ͼ��ʱ���������Ƿ���Ȼ����������������֤����������������˵������.
(2)��ͼ���е�![]() �Ƶ�A��ת��DE��ֱ��AC��ֱ��ֱ��BD��CE�ڵ�F����
�Ƶ�A��ת��DE��ֱ��AC��ֱ��ֱ��BD��CE�ڵ�F����![]() ��
��![]() ���뻭��ͼ�Σ������BF�ij�.
���뻭��ͼ�Σ������BF�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
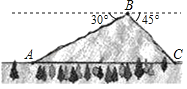
����Ŀ������304����ͨ�������ֹ��ն����������о���һ��ɽ�壬��ͼ��ʾ������ɽ��A��C���غ��θ߶�ԼΪ1000�ף�ɽ��B���ĺ��θ߶�ԼΪ1400�ף���B����ɽ��A���ĸ���Ϊ30������B����ɽ��C���ĸ���Ϊ45��������A��C���ؼ��ͨһ���������������Ϊ�����ף����ȡ�������ο�����![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����x�����������A��B�ĺ�����ֱ�Ϊ��3��1����y�ύ�ڵ�C�������ĸ����ۣ���16a+4b+c��0������P����5��y1����Q��![]() ��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����c=��3a��������ABC�ǵ��������Σ���b=��
��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����c=��3a��������ABC�ǵ��������Σ���b=��![]() ��
��![]() ��������ȷ����_____�����뽫��ȷ���۵����ȫ�����ں����ϣ�
��������ȷ����_____�����뽫��ȷ���۵����ȫ�����ں����ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com