
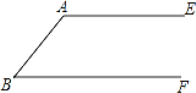
【题目】如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明
(1)用直尺和圆规作出∠ABF的平分线BD交AE于点D,再作出BD的中点O(不写作法,保留作图痕迹)
(2)连接(1)所作图中的AO并延长与BF相交于点C,连接DC,求证:四边形ABCD是菱形.
【答案】(1)、答案见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据角平分线的作法和中点的作法得出答案;(2)、首先证明△ADO与△CBO全等,从而得出四边形ABCD为平行四边形,然后根据BD平分∠ABC得出∠ABD=∠CBD,根据AE∥BF得出∠ABD=∠ADB,从而得出AB=AD,根据点O是BD的中点得出对角线互相垂直,从而得出菱形.
试题解析:(1)、如图.
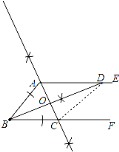
(2)、∵AE∥BF,∴∠ADO=∠CBO.在△ADO与△CBO中,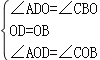 ,
,
∴△ADO≌△CBO(ASA),∴AD=BC, ∴四边形ABCD是平行四边形.
∵BD平分∠ABC,∴∠ABD=∠CBD.又∵AE∥BF,
∴∠ABD=∠ADB,∴AB=AD.又∵点O是BD的中点,∴AO⊥BD,即AC⊥BD.
∴平行四边形ABCD是菱形.


科目:初中数学 来源: 题型:
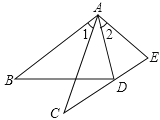
【题目】在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设:___________;结论:_______.(均填写序号)
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①DF=DN ②AE=CN;③△DMN是等腰三角形;④∠BMD=45°,其中正确的结论个数是 ( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=3x2向左平移1个单位,再向下平移2个单位,所得到的抛物线是 ( )
A. y=3(x-1)2-2 B. y=3(x+1)2-2
C. y=3(x+1)2+2 D. y=3(x-1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数,用负数记下降数).那么本周星期几水位最低( )
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | 0.12 | ﹣0.02 | ﹣0.13 | ﹣0.20 | ﹣0.08 | ﹣0.02 | 0.32 |
A. 星期二 B. 星期四 C. 星期六 D. 星期五
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级准备购买一批笔奖励优秀学生,在购买时发现,每只笔可以打九折,用360元钱购买的笔,打折后购买的数量比打折前多10本.
(1)求打折前每支笔的售价是多少元?
(2)由于学生的需求不同,学校决定购买笔和笔袋共80件,笔袋每个原售价为10元,两种物品都打八折,若购买总金额不低于400元,问最多购买多少支笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
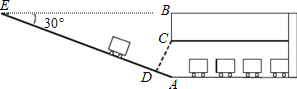
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米,![]() =1.732).
=1.732).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com