【题目】关于x的一元二次方程x2+bx+c＝0的两根为x1＝1，x2＝2，则x2+bx+c分解因式的结果为_____．
赢在课堂名师课时计划系列答案科目：初中数学 来源： 题型：
【题目】勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪灵感.他惊喜地发现：当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1摆放，其中∠DAB=90°，求证：a2+b2=c2.
证明：连接DB，过点D作BC边上的高DF，则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=
b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b－a)，
∴b2+ab=c2+a(b－a)，
∴a2+b2=c2.
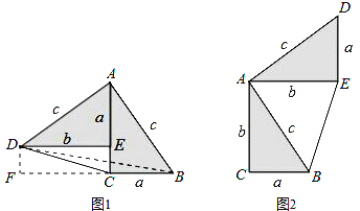
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°.
求证：a2+b2=c2.
证明：连接 ，
∵S五边形ACBED= ，
又∵S五边形ACBED= ，
∴ ，
∴a2+b2=c2.
查看答案和解析>>
科目：初中数学 来源： 题型：
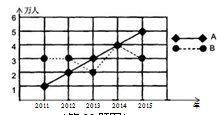
【题目】如图所示，A、B两个旅游点从2011年至2015年“清明小长假”期间的旅游人数变化情况分别用实线和虚线表示，请解答以下问题：
（1）B旅游点的旅游人数相对上一年，增长最快的是哪一年？
（2）求A、B两个旅游点从2011年到2015年旅游人数的平均数和方差，并从平均数和方差的角度，用一句话对这两个旅游点的情况进行评价；
（3）A旅游点现在的门票价格为每人80元，为保护旅游点环境和游客的安全，A旅游点的最佳接待人数为4万人. A旅游点决定提高门票价格来控制游客数量. 已知游客数量y（万人）与门票价格x（元）之间满足函数关系
. 若要使A旅游点的游客人数不超过4万人，则门票价格至少应提高多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
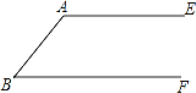
【题目】如图，AE∥BF，先按（1）的要求作图，再按（2）的要求证明
（1）用直尺和圆规作出∠ABF的平分线BD交AE于点D，再作出BD的中点O（不写作法，保留作图痕迹）
（2）连接（1）所作图中的AO并延长与BF相交于点C，连接DC，求证：四边形ABCD是菱形．
查看答案和解析>>
科目：初中数学 来源： 题型：
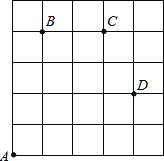
【题目】如图，一只甲虫在5×5的方格（每小格边长为1个单位长度）上沿着网格线运动，它从A处出发去看望B、C、D处的其它甲虫．规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从D到C记为：D→C（﹣1，+2），其中第一个数表示左右方向，第二个数表示上下方向．
（1）图中A→C可以记为（ ， ），B→C可以记为（ ， ）．
（2）D→ 可以记为（﹣4，﹣2）．
（3）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程长度为 ；
（4）若这只甲虫从A处去甲虫P处的行走路线依次为（+1，+3），（+3，﹣2），（﹣2，+1），请在图中标出P的位置．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1是“东方之星”救援打捞现场图，小红据此构造出一个如图2所示的数学模型，已知：A、B、D三点在同一水平线上，CD⊥AD，∠A=30°，∠CBD=75°，AB=60m．
（1）求点B到AC的距离；
（2）求线段CD的长度．
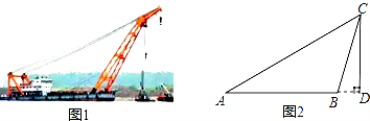
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
