
已知二次函数y=﹣x2﹣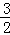 x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )
x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )
A.y1<0,y2<0 B.y1<0,y2>0 C.y1>0,y2<0 D.y1>0,y2>0
 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
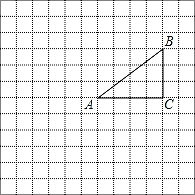
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△AB C的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
C的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
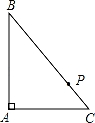
如图,P是Rt△ABC的斜边BC上异于B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )
A.1条 B.2条 C.3条 D.4条
查看答案和解析>>
科目:初中数学 来源: 题型:
用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100 B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣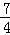 )2=
)2=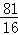 D.3x2﹣4x﹣2=0化为(x﹣
D.3x2﹣4x﹣2=0化为(x﹣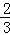 )2=
)2=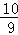
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,∠ACB=90°.经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、点A作直线l的垂线,垂足分别为点D、点E.
(1)若∠ABC=45°,CD=1(如图),则AE的长为 ;
(2)写出线段AE、CD之间的数量关系,并加以证明;
(3)若直线CE、AB交于点F,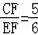
 ,CD=4,求BD的长.
,CD=4,求BD的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com