
【题目】如图,抛物线y=ax2+bx-4a的对称轴为直线x=![]() ,与x轴交于A,B两点,与y轴交于点C(0,4).
,与x轴交于A,B两点,与y轴交于点C(0,4).

(1)求抛物线的解析式,结合图象直接写出当0≤x≤4时y的取值范围;
(2)已知点D(m,m+1)在第一象限的抛物线上,点D关于直线BC的对称点为点E,求点E的坐标.
【答案】(1)0≤y≤![]() .(2)(0,1).
.(2)(0,1).
【解析】
试题分析:(1)把C(0,4)代入y=ax2+bx-4a得出a=-1,由对称轴得出b=3,即可得出抛物线的解析式;结合图象容易得出当0≤x≤4时y的取值范围;
(2)把点D(m,m+1)代入抛物线解析式,求出m的值;由题意得出CD∥AB,且CD=3,再证明△OBC是等腰直角三角形,得出∠OCB=∠DCB=45°,得出点E在y轴上,OE=1,即可得出点E的坐标.
试题分析:(1)将C(0,4)代入y=ax2+bx-4a中得a=-1
又∵对称轴为直线x=![]() ,
,
∴-![]() =
=![]() ,得b=3.
,得b=3.
∴抛物线的解析式为y=-x2+3x+4,
∵y=-x2+3x+4=-(x-![]() )2+
)2+![]() .
.
∴顶点坐标为:(![]() ,
,![]() ),
),
∴当0≤x≤4时y的取值范围是0≤y≤![]() .
.
(2)∵点D(m,m+1)在抛物线上,
∴m+1=-m2+3m+4,
解得:m=-1,或m=3;
∵点D在第一象限,
∴点D的坐标为(3,4).
又∵C(0,4),
∴CD∥AB,且CD=3.
当y=-x2+3x+4=0时,
解得:x=-1,或x=4,
∴B(4,0);
当x=0时,y=4,
∴C(0,4),
∴OB=OC=4,
∴∠OCB=∠DCB=45°,
∴点E在y轴上,且CE=CD=3,
∴OE=1.
即点E的坐标为(0,1).



科目:初中数学 来源: 题型:
【题目】某商品原价800元,连续两次降价a%后售价为578元,下列所列方程正确的是( )
A. 800(1+a%)2=578 B. 800(1-a%)2="578" C. 800(1-2a%)=578 D. 800(1-a2%)=578
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年师大附中秋季运动会,为了准备入场式,初一年级某班买了两种布料共28米,花了88元.其中黄布料每米3元,红布料每米3.5元,该班两种布料各买了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
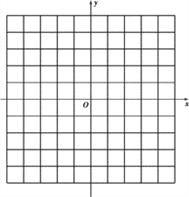
【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)
(1) 描出A、B、C、D、四点的位置,并顺次连接ABCD,
(2) 四边形ABCD的面积是________.
(3) 把四边形ABCD向左平移5个单位,再向下平移2个单位得到四边形A'B'C'D',写出点A'、B'、C'、D'的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com