
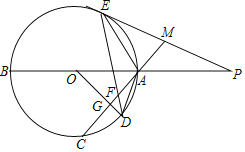
【题目】如图,已知AB是⊙O的直径,AC是弦(不是直径),OD⊥AC垂足为G交⊙O于D,E为⊙O上一点(异于A、B),连接ED交AC于点F,过点E的直线交BA、CA的延长线分别于点P、M,且ME=MF.
(1)求证:PE是⊙O的切线.
(2)若DF=2,EF=8,求AD的长.
(3)若PE=6![]() ,sin∠P=
,sin∠P=![]() ,求AE的长.
,求AE的长.
【答案】(1)详见解析;(2)![]() ;(3)2
;(3)2![]() .
.
【解析】
(1)连接OE,根据余角的性质和等腰三角形的性质得到∠D=∠OED,求得OE⊥PE,于是得到结论;
(2)根据垂径定理得到![]() ,求得∠FAD=∠AED,根据相似三角形的性质得到结论;
,求得∠FAD=∠AED,根据相似三角形的性质得到结论;
(3)设OE=x,解直角三角形即可得到结论.
(1)证明:连接OE,
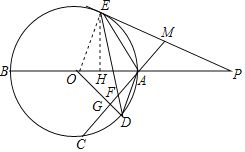
∵OD⊥AC,
∴∠DGF=90°,
∴∠D+∠DFG=∠D+∠AFE=90°,
∴∠DFG=∠AFE,
∵ME=MF,
∴∠MEF=∠MFE,
∵OE=OD,
∴∠D=∠OED,
∴∠OED+∠MEF=90°,
∴OE⊥PE,
∴PE是⊙O的切线;
(2)∵OD⊥AC,
∴![]() ,
,
∴∠FAD=∠AED,
∵∠ADF=∠EDA,
∴△DFA~△DAE,
∴![]() ,
,
∴AD2=DFDE=2×10=20,
∴AD=2![]() ;
;
(3)解:设OE=x,
∵sin∠P=![]() ,
,
∴OP=3x,
∴x2+(6![]() )2=(3x)2,
)2=(3x)2,
解得:x=3,
过E作EH垂直AB于H,
sin∠P=![]() ,
,
∴EH=2![]() ,
,
∵OH2+EH2=OE2,
∴OH=1,∴AH=2,
∵AE2=HE2+AH2,
∴AE=2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
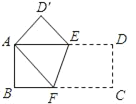
【题目】如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A、C重合,若其长BC为8,宽AB为4.
(1)求证:△AEF是等腰三角形.
(2)EF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
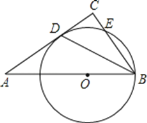
【题目】如图:在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E。
(1)试说明:AC是⊙O的切线;
(2)若BC=6,tan∠A=![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
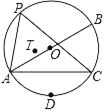
【题目】如图,AB为⊙O的直径,点C、D分别是半圆AB的三等分点,AB=4,点P自A点出发,沿弧ABC向C点运动,T为△PAC的内心.当点P运动到使BT最短时就停止运动,点T运动的路径长为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
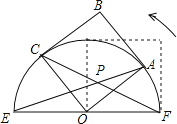
【题目】如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
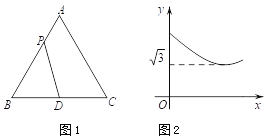
【题目】如图1,在等边△ABC中,点D是BC边的中点,点P为AB边上的一个动点,设![]() ,图1中线段DP的长为
,图1中线段DP的长为![]() ,若表示
,若表示![]() 与
与![]() 的函数关系的图象如图2所示,则等边△ABC的面积为_____.
的函数关系的图象如图2所示,则等边△ABC的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com