
 如图,△ABC中,AB=AC,∠A=30°,AB的垂直平分线MN交AC于D,则∠DBC的度数为( )
如图,△ABC中,AB=AC,∠A=30°,AB的垂直平分线MN交AC于D,则∠DBC的度数为( )| A、60° | B、45° |
| C、40° | D、30° |
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
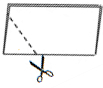 如图,将一张矩形纸片对折两次后剪下一个角,然后打开.如果要剪出一个正方形,那么剪口线与折痕所成的锐角大小是( )
如图,将一张矩形纸片对折两次后剪下一个角,然后打开.如果要剪出一个正方形,那么剪口线与折痕所成的锐角大小是( )| A、22.5° | B、45° |
| C、60° | D、135° |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
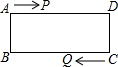 如图,在矩形ABCD中,AD=12cm,点P从点A到点D以每秒1cm的速度运动,点Q以每秒4cm的速度从点C出发向点B运动,并在B、C两点之间做来回运动,两点同时出发,点P到达点D时P、Q停止运动,当线段PQ∥AB时,AP的长可以是
如图,在矩形ABCD中,AD=12cm,点P从点A到点D以每秒1cm的速度运动,点Q以每秒4cm的速度从点C出发向点B运动,并在B、C两点之间做来回运动,两点同时出发,点P到达点D时P、Q停止运动,当线段PQ∥AB时,AP的长可以是查看答案和解析>>
科目:初中数学 来源: 题型:
| A、①③ | B、②③ | C、③④ | D、②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,A(-1,-3),OB=
如图,在平面直角坐标系中,A(-1,-3),OB=| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
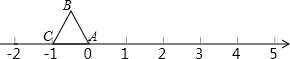
| A、不对应任何数 |
| B、对应的数是2013 |
| C、对应的数是2014 |
| D、对应的数是2015 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com