
【题目】已知:直线MN,PQ被射线BA截于A,B两点,且MN∥PQ,点D是直线MN上一定点,C是射线BA上一动点,连结CD,过点C作CE⊥CD交直线PQ于点E.

(1)若点C在线段AB上.
①依题意,补全图形;
②请写出∠ADC和∠CEB的数量关系,并证明.
(2)若点C在线段BA的延长线上,直接写出∠ADC和∠CEB的数量关系,不必证明.
【答案】(1)①见解析;②∠ADC和∠CEB的数量关系:∠ADC+∠CEB=90°;证明见解析;(2)∠ADC+∠CEB=90°或∠CEB-∠ADC=90或∠ADC-∠CEB=90°
【解析】
(1)①连接CD,作CE⊥CD,交PQ于E即可;
②根据两直线平行,内错角相等可知∠DCH=∠ADC,∠ECH=∠CEB,由∠DCH+∠ECH=90°,可知∠ADC+∠CEB=90°;
(2)利用平行线的性质,三角形外角的性质,平角的定义列式即可求得.
(1)①补全图形,如图.
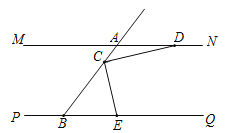
②∠ADC和∠CEB的数量关系:∠ADC+∠CEB=90°.
证明:如图1,过点C作CH∥MN.
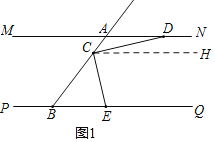
∴∠DCH=∠ADC,∠ECH=∠CEB.
∵CD⊥CE,
∴∠DCE=90°,即∠DCH+∠ECH=90°.
∴∠ADC+∠CEB=90°.
(2)如图2①,
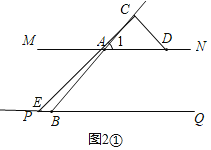
∵CE⊥CD,
∴∠1+∠ADC=90°,
∵MN∥PQ,
∴∠1=∠CEB,
∴∠ADC+∠CEB=90°;
如图2②,
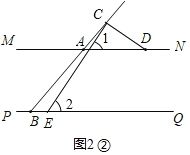
∵CE⊥CD,
∴∠1+∠ADC=90°,
∵MN∥PQ,
∴∠1=∠2,
∵∠2+∠CEB=180°,
∴90°-∠ADC+∠CEB=180°,
∴∠CEB-∠ADC=90°;
如图2③,
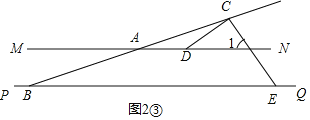
∵CE⊥CD,
∴∠ECD=90°,
∵MN∥PQ,
∴∠1=∠CEB,
∵∠ADC=∠ECD+∠1,
∴∠ADC=90°+∠CEB
∴∠ADC-∠CEB=90°;
综上,∠ADC和∠CEB的数量关系为:∠ADC+∠CEB=90°或∠CEB-∠ADC=90°或∠ADC-∠CEB=90°.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是⊙O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校青年老师准备捐款3600元为敬老院的老年人购买一台电脑,这笔钱大家平均承担.实际捐款时又多了2名教师,因为购买电脑所需的总费用不变,于是每人少捐90元.问共有多少人参加捐款?原计划每人捐款多少元?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
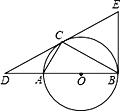
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“※”定义一种新运算:对于任意有理数a和b,规定a※b=ab2+2ab+a.
如:1※2=1×22+2×1×2+1=9
(1)(﹣2)※3= ;
(2)若![]() ※3=16,求a的值;
※3=16,求a的值;
(3)若2※x=m,(![]() x)※3=n(其中x为有理数),试比较m,n的大小.
x)※3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com