
已知:如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?
请证明你的结论.
 |
科目:初中数学 来源: 题型:
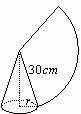
如图,用一个半径为30cm,面积为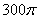 cm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径
cm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径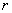 为【 】
为【 】
A. 5cm B. 10cm C. 20cm D. 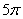 cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
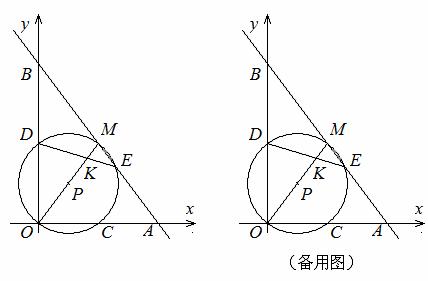
如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交 轴,
轴, 轴的正半轴于A,B两点,且M是AB的中点. 以OM为直径的⊙P分别交
轴的正半轴于A,B两点,且M是AB的中点. 以OM为直径的⊙P分别交 轴,
轴, 轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.
轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.
(1)若点M的坐标为(3,4),①求A,B两点的坐标; ②求ME的长;
(2)若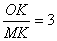 ,求∠OBA的度数;
,求∠OBA的度数;
(3)设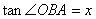 (0<
(0< <1),
<1),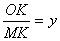 ,直接写出
,直接写出 关于
关于 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数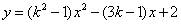 .
.
(1)二次函数的顶点在 轴上,求
轴上,求 的值;
的值;
(2)若二次函数与 轴的两个交点A、B均为整数点(坐标为整数的点),当
轴的两个交点A、B均为整数点(坐标为整数的点),当 为整数时,求A、B两点的坐标.
为整数时,求A、B两点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com