
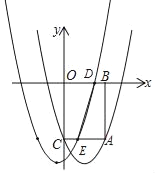
【题目】已知抛物线y=x2+bx+c经过点A(2,﹣3).
(1)如图,过点A分别向x轴,y轴作垂线,垂足分别为B,C,得到矩形ABOC,且抛物线经过点C.
①求抛物线的解析式.
②将抛物线向左平移m(m>0)个单位,分别交线段OB,AC于D,E两点.若直线DE刚好平分矩形ABOC的面积,求m的值.
(2)将抛物线平移,使点A的对应点为A1(2﹣n,3b),其中n≥1.若平移后的抛物线仍然经过点A,求平移后的抛物线顶点所能达到最高点时的坐标.

【答案】(1)①y=x2﹣2x﹣3;②m=![]() ;(2)顶点坐标(0,﹣7).
;(2)顶点坐标(0,﹣7).
【解析】
(1)①将A(2,﹣3),B(2,0)代入y=x2+bx+c即可求出;
②因为直线DE刚好平分矩形ABOC的面积,所以AE=OD=m,DB=CE=2﹣m,D(m,0),E(2﹣m,﹣3),易知F(3,0),所以DF=3﹣m,于是3﹣m=m,从而求出m;
(2)由抛物线y=x2+bx+c经过点A(2,﹣3),可得y=x2+bx﹣2b﹣7,由A的对应点为A1(2﹣n,3b),可知抛物线向左平移了n个单位,向上平移(3b+3)个单位,则平移后y=(x+n)2+b(x+n)﹣2b﹣7+3b+3,整理后根据平移后的抛物线仍然经过点A(2,﹣3),继而可求得b=﹣n﹣1,进而可求得顶点坐标.
(1)①∵四边形ABOC是矩形,A(2,﹣3),
∴B(2,0),C(0.﹣3),
∵抛物线y=x2+bx+c过点A、C,
∴![]() , 解得:
, 解得:![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3;
②如图,设原抛物线与x轴正半轴交于点F,
∵直线DE刚好平分矩形ABOC的面积,
∴AE=OD=m,DB=CE=2﹣m
∴D(m,0),E(2﹣m,﹣3)
∵易知F(3,0),
∴DF=3﹣m,
∵DF=AE,
∴3﹣m=m,
∴m=![]() ;
;
(2)抛物线y=x2+bx+c经过点A(2,﹣3).
﹣3=22+2b+c,
∴c=﹣2b﹣7,
∴y=x2+bx﹣2b﹣7,
∵A的对应点为A1(2﹣n,3b),
∴抛物线向左平移了n个单位,向上平移(3b+3)个单位
则平移后y=(x+n)2+b(x+n)﹣2b﹣7+3b+3,
整理得y=(x+n)2+b(x+n)+b﹣4=(x+n+![]() )2﹣
)2﹣![]() +b﹣4,
+b﹣4,
∵平移后的抛物线仍然经过点A(2,﹣3),
∴﹣3=(2+n)2+b(2+n)+b﹣4,
∴n2+4n+3+b(3+n)=0,
∴(n+1(n+3))+b(n+3)=0,
(
∵n≥1,∴n+3>0,
∴n+1+b=0,b=﹣n﹣1,
顶点坐标(﹣n﹣![]() ,﹣
,﹣![]() +b﹣4),
+b﹣4),
y顶=﹣![]() +b﹣4=﹣
+b﹣4=﹣![]() (b﹣2)2﹣3=﹣
(b﹣2)2﹣3=﹣![]() (n+3)2﹣3,
(n+3)2﹣3,
∵n≥1,-![]() <0,
<0,
∴n=1时,顶点最高,此时b=﹣1﹣1=﹣2,
顶点坐标(0,﹣7).


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】定义:有一组对角互补的四边形叫做互补四边形.
![]() 概念理解:
概念理解:
①在互补四边形![]() 中,
中,![]() 与
与![]() 是一组对角,若
是一组对角,若![]() 则
则![]() _
_ ![]()
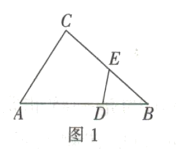
②如图1,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,且
上,且![]() 求证:四边形
求证:四边形![]() 是互补四边形.
是互补四边形.
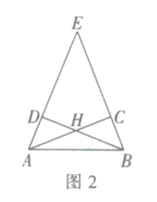
![]() 探究发现:如图2,在等腰
探究发现:如图2,在等腰![]() 中,
中,![]() 点
点![]() 分别在边
分别在边![]() 上,
上, ![]() 四边形
四边形![]() 是互补四边形,求证:
是互补四边形,求证:![]() .
.
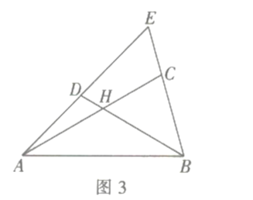
![]() 推广运用:如图3,在
推广运用:如图3,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,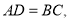 四边形
四边形![]() 是互补四边形,若
是互补四边形,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.
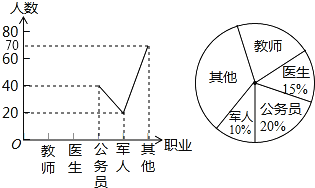
(1)把折线统计图补充完整;
(2)求出扇形统计图中,公务员部分对应的圆心角的度数;
(3)若从被调查的学生中任意抽取一名,求取出的这名学生最喜欢的职业是“教师”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平直角坐标系中,规定:抛物线![]()
![]() 的相关直线为
的相关直线为![]() .例如:二次函数
.例如:二次函数![]() 的相关直线为
的相关直线为![]() .
.

(1)直接写出抛物线![]() 的相关直线,并求出抛物线
的相关直线,并求出抛物线![]() 与其相关直线的交点坐标;
与其相关直线的交点坐标;
(2)如图,抛物线![]()
![]() 与它的相关直线
与它的相关直线![]() 交于
交于![]() 、
、![]() 两点.
两点.
①求抛物线的解析式;
②连结![]() ,求
,求![]() 的面积;
的面积;
③作![]() ,过抛物线上一动点
,过抛物线上一动点![]() (不与
(不与![]() 、
、![]() 重合)作直线
重合)作直线![]() 的平行线交
的平行线交![]() 于点
于点![]() ,若以点
,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,直接写出点
为顶点的四边形是平行四边形,直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
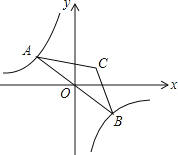
【题目】如图,已知反比例函数y=﹣![]() 的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为__.
的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲、乙两台机器加工同一种零件,已知一小时甲加工的零件数与一小时乙加工的零件数的和为36个,甲加工80个零件与乙加工100个零件的所用时间相等.求甲、乙两台机器每小时分别加工零件多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .直线
.直线![]() 与
与![]()
![]()
![]() 交于点
交于点![]() .记线段
.记线段![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .横,纵坐标都是整数的点叫做整点.
.横,纵坐标都是整数的点叫做整点.
(1)当![]() 时,区域
时,区域![]() 内的整点个数为_____;
内的整点个数为_____;
(2)若区域![]() 内没有整点,则
内没有整点,则![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
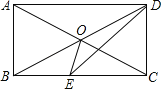
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)
如图1,在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() 平行于
平行于![]() .
.![]() ,点
,点![]() 在直线
在直线![]() 上移动,角的一边
上移动,角的一边![]() 始终经过点
始终经过点![]() ,另一边
,另一边![]() 与
与![]() 交于点
交于点![]() ,研究
,研究![]() 和
和![]() 的数量关系.
的数量关系.
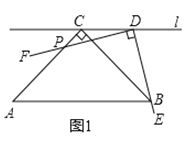
(探究发现)
(1)如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点![]() 移动到使点
移动到使点![]() 与点
与点![]() 重合时,通过推理就可以得到
重合时,通过推理就可以得到![]() ,请写出证明过程;
,请写出证明过程;
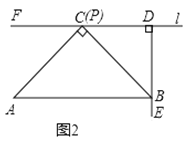
(数学思考)
(2)如图3,若点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() ),受(1)的启发,这个小组过点
),受(1)的启发,这个小组过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,就可以证明
,就可以证明![]() ,请完成证明过程;
,请完成证明过程;
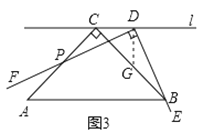
(拓展引申)
(3)如图4,在(1)的条件下,![]() 是
是![]() 边上任意一点(不含端点
边上任意一点(不含端点![]() ),
),![]() 是射线
是射线![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,这个数学兴趣小组经过多次取
,这个数学兴趣小组经过多次取![]() 点反复进行实验,发现点
点反复进行实验,发现点![]() 在某一位置时
在某一位置时![]() 的值最大.若
的值最大.若![]() ,请你直接写出
,请你直接写出![]() 的最大值.
的最大值.
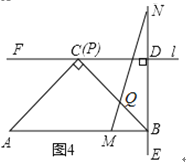
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com