
【题目】已知关于x的方程mx2﹣(3m﹣1)x+2m﹣2=0
(1)求证:无论m取任何实数时,方程恒有实数根;
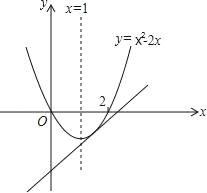
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2,且抛物线的开口向上时,求此抛物线的解析式;
(3)在坐标系中画出(2)中的函数图象,分析当直线y=x+b与(2)中的图象只有两个交点时b的取值范围.
【答案】(1)见解析; (2)所求抛物线的解析式为:y=x2﹣2x;(3)当b>﹣![]() 时,直线y=x+b与(2)中的图象只有两个交点.
时,直线y=x+b与(2)中的图象只有两个交点.
【解析】试题分析:(1)二次项系数m的值不确定,分为m=0,m≠0两种情况,分别证明方程有实数根;
(2)设抛物线与x轴两交点的横坐标为x1,x2,则两交点之间距离为|x1-x2|=2,再与根与系数关系的等式结合变形,可求m的值,从而确定抛物线的解析式;
(3)联立方程组,有解时,求出b的取值范围.
试题解析:
(1)分两种情况讨论.
①当m=0时,方程为x﹣2=0,x=2.
∴m=0时,方程有实数根.
②当m≠0时,则一元二次方程的根的判别式
△=[﹣(3m﹣1)]2﹣4m(2m﹣2)
=9m2﹣6m+1﹣8m2+8m=m2+2m+1
=(m+1)2≥0,
∴m≠0时,方程有实数根.
故无论m取任何实数时,方程恒有实数根.
综合①②可知,m取任何实数,方程mx2﹣(3m﹣1)x+2m﹣2=0恒有实数根;
(2)设x1,x2为抛物线y=mx2﹣(3m﹣1)x+2m﹣2与x轴交点的横坐标.
则有x1+x2=![]() ,x1x2=
,x1x2=![]()
由|x1﹣x2|=![]() =|
=|![]() |,
|,
由|x1﹣x2|=2得|![]() |=2,
|=2,
∴![]() =2或
=2或![]() =﹣2
=﹣2
∴m=1或m=﹣![]()
而抛物线开口向上,
∴m=1
∴所求抛物线的解析式为:y=x2﹣2x;
(3)在(2)的条件下,直线y=x+b与抛物线y1,y2组成的图象只有两个交点,
联立得, ![]() ,
,
∴x2﹣3x﹣b=0,
∴△=9+4b>0,解得b>﹣![]() ;
;
当b>﹣![]() 时,直线y=x+b与(2)中的图象只有两个交点.
时,直线y=x+b与(2)中的图象只有两个交点.


科目:初中数学 来源: 题型:
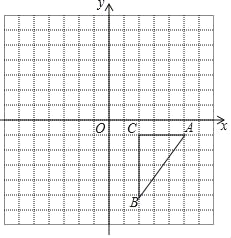
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的小正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A,B,C三点的坐标分别为(5,﹣1),(2,﹣5),(2,﹣1).
(1)把△ABC向上平移6个单位后得到△A1B1C1,画出△A1B1C1;
(2)画出△A2B2C2,使它与△ABC关于y轴对称;
(3)画出△A3B3C3,使它与△ABC关于原点中心对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
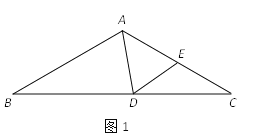
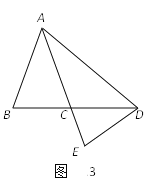
【题目】在△ABC中,∠ABC=∠ACB,点D在BC边所在的直线上,点E在射线AC上,且始终保持∠ADE=∠AED.
(1)如图1,若∠B=∠C=30°,∠BAD=70°,求∠CDE的度数;
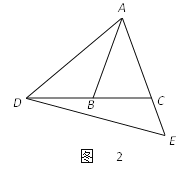
(2)如图2,若∠ABC=∠ACB=70°,∠CDE=15°,求∠BAD的度数;
(3)如图3,当点D在BC边的延长线上时,猜想∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过A(2,0),B(0,-6)两点.
的图象经过A(2,0),B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
(3)在x轴上是否存在一点P,使△ABP为等腰三角形,若存在,求出P的坐标,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
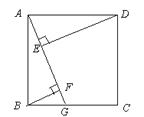
【题目】如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1) 求证:DE-BF = EF;
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊿ABC中,∠A=40°,∠ACB=104°,BD为AC边上的高,BE是⊿ABC的角平分线,求∠EBD的度数.
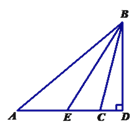
【答案】32°
【解析】试题分析:根据三角形的内角和定理求出∠ABC,再根据角平分线的定义求出∠ABE,然后利用三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BED,再根据直角三角形两锐角互余列式进行计算即可得解.
试题解析:由三角形内角和定理,得∠B+∠ACB+∠BAC=180°,
又∠A=40°,∠ACB=104°,
∴∠ABC=180°-40°-104°=36°,
又∵BE平分∠ABC,
∴∠ABE=![]() ∠ABC=18°
∠ABC=18°
∴∠BED=∠A+∠ABE=40°+18°=58°,
又∵∠BED+∠DBE=90°,
∴∠DBE=90°-∠BED=90°-58°=32°.
【题型】解答题
【结束】
25
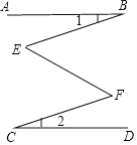
【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在网络阅读成为主流的同时,进实体书店看书买书也成为一种新的时尚,重庆杨家坪某书店打算购进一批网络畅销书籍进行销售.该书店用12000元购进甲种书籍,用14400元购进乙种书籍,且购进甲乙两种书籍数量相同,甲的进价每本比乙少2元.
(1)求甲乙两种书籍进价分别每本多少元?
(2)随着抖音等网络视频软件的推广,这个书店很快成为网红书店,人流量越来越大.甲种书籍按每15元很快销售一空,书店决定再次购进甲种书籍进行销售.由于纸张成本增加,甲种书籍第二次比第一次进价每本增加20%,第二次购进甲种书籍总量在第一次购进甲种书籍总量的基础上増加了a%(a>0),为了让利于读者,第二次销售单价在第一次的基础上减少了![]() %,结果第二次全部售完甲种书籍的利润达到3600元.求a的值.
%,结果第二次全部售完甲种书籍的利润达到3600元.求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com