
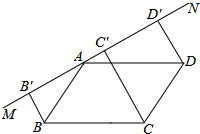
 已知:如图,直线MN经过?ABCD的顶点A,BB′⊥MN,CC′⊥MN,DD′⊥MN,B′、C′、D′是垂足.
已知:如图,直线MN经过?ABCD的顶点A,BB′⊥MN,CC′⊥MN,DD′⊥MN,B′、C′、D′是垂足.分析 (1)如图1中,连接AC、BD交于点O,作OO′⊥MN于O′,利用三角形中位线定理以及梯形中位线定理即可证明.
(2)(ⅰ)如图2中,结论AA′+CC′=BB′+DD,连接AC、BD交于点O,作OO′⊥MN于OO′,利用梯形中位线定理可以证明AA′+CC′=BB′+DD.
(ⅱ)如图3中,结论CC′-AA′=BB′+DD,连接AC、BD交于点O,作OO′⊥MN于OO′,延长A′O交CC′于E,只要证明CC′-AA′=2OO′.BB′+DD′=2OO′即可.
(ⅲ)如图4中,结论CC′-AA′=DD′-BB,连接AC、BD交于点O,作OO′⊥MN于OO′,证明方法类似.
解答 (1)证明:如图1中,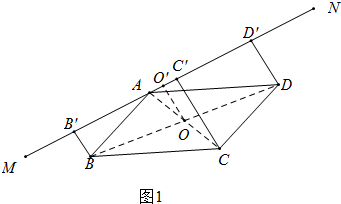 连接AC、BD交于点O,作OO′⊥MN于O′.
连接AC、BD交于点O,作OO′⊥MN于O′.
∵四边形ABCD是平行四边形,
∴AO=OC,BO=BD,
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,
∴BB′∥OO′∥CC′∥DD′,
∴B′O′=O′D′,AO′=O′C′,
∴CC′=2OO′,BB′+DD′=2OO′,
∴CC′=BB′+DD′.
(2)(ⅰ)当点A、B、C、D都在直线MN的同一侧,
如图2中,连接AC、BD交于点O,作OO′⊥MN于OO′,
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,AA′⊥MN,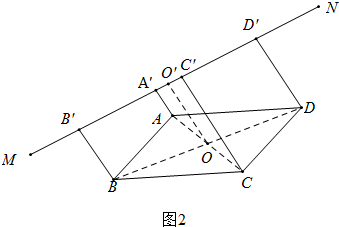
∴BB′∥OO′∥CC′∥DD′∥AA′,
∴B′O′=O′D′,A′O′=O′C′,
∴AA′+CC′=2OO′,BB′+DD′=2OO′,
∴AA′+CC′=BB′+DD′,
故答案为AA′+CC′=BB′+DD′
(ⅱ)当A点在MN的一侧,点B、C、D在另一侧,如图3中,
如图3中,连接AC、BD交于点O,作OO′⊥MN于OO′,延长A′O交CC′于E.
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,AA′⊥MN,
∴BB′∥OO′∥CC′∥DD′∥AA′,
∴B′O′=O′D′,A′O′=O′C′,
∴BB′+DD′=2OO′,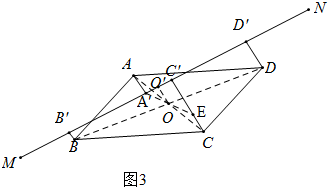 ∵AA′∥CE,
∵AA′∥CE,
∴∠AA′O=∠OEC$\left\{\begin{array}{l}{∠AOA′=∠EOC}\\{∠AA′O=∠OEC}\\{AO=OC}\end{array}\right.$,
在△AA′O和△CEO中,
$\left\{\begin{array}{l}{∠AOA′=∠EOC}\\{∠AA′O=∠OEC}\\{AO=OC}\end{array}\right.$,
∴△AA′O≌△CEO,
∴AA′=EC,A′O=OE,
∴EC′=2OO′,即CC′-AA′=2OO′,
∴CC′-AA′=BB′+DD′,
故答案为CC′-AA′=BB′+DD.
(ⅲ)当点A、B在MN的一侧,点C、D在另一侧,
如图4中,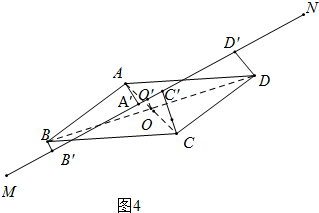 连接AC、BD交于点O,作OO′⊥MN于OO′,
连接AC、BD交于点O,作OO′⊥MN于OO′,
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,AA′⊥MN,
∴BB′∥OO′∥CC′∥DD′∥AA′,
∴B′O′=O′D′,A′O′=O′C′,
同理可以证明:CC′-AA′=2OO′,DD′-BB′=2OO′,
∴CC′-AA′=DD′-BB′,
故答案为CC′-AA′=DD′-BB′.
点评 本题考查平行四边形的性质、三角形的中位线定理、梯形的中位线定理、全等三角形的判定和性质,解题的关键是正确添加辅助线,利用中位线定理解决问题,题目有点难度,学会转化的思想,把问题转化为三角形中位线、梯形中位线解决.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:填空题
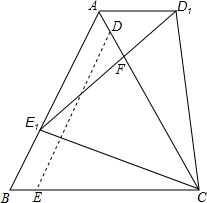 如图,在等边△ABC与等边△CDE中D、E分别在边AC、BC上,且DE∥AB,BC=4$\sqrt{3}$,CE=$\sqrt{39}$,将△CED绕着C点顺时针旋转到△CD1E1,记线段AC与线段E1D1的交点为F,当E点落在AB边上的时候停止旋转,问此时CF的长为$\frac{13}{4}$$\sqrt{3}$.
如图,在等边△ABC与等边△CDE中D、E分别在边AC、BC上,且DE∥AB,BC=4$\sqrt{3}$,CE=$\sqrt{39}$,将△CED绕着C点顺时针旋转到△CD1E1,记线段AC与线段E1D1的交点为F,当E点落在AB边上的时候停止旋转,问此时CF的长为$\frac{13}{4}$$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com