
分析 (1)根据题目所给信息求解;
(2)根据[2.5]=2,[3]=3,[-2.5]=-3,可得[x]=2中的2≤x<3,根据<a>表示大于a的最小整数,可得<y>=-1中,-2≤y<-1;
(3)根据题意得出3≤$\frac{x+1}{2}$<4,求出x的取值范围,从而得出满足条件的所有正整数的解;
(4)先求出[x]和<y>的值,然后求出x和y的取值范围.
解答 解:(1)由题意得:[-4.5]=-5,<3.5>=4;
(2)∵[x]=2,
∴x的取值范围是2≤x<3;
∵<y>=-1,
∴y的取值范围是-2≤y<-1;
(3)根据题意得:3≤$\frac{x+1}{2}$<4,
解得:5≤x<7,
则满足条件的所有正整数为5,6.
(4)解方程组得:$\left\{\begin{array}{l}{[x]=-1}\\{<y>=3}\end{array}\right.$,
故x,y的取值范围分别为-1≤x<0,2≤y<3.
故答案为:-5,4;2≤x<3,-2≤y<-1.
点评 本题考查了一元一次不等式组的应用,解答本题的关键是读懂题意,根据题目所给的信息进行解答.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
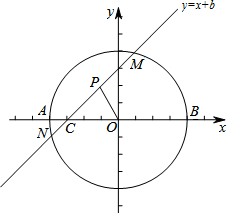 如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )
如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )| A. | 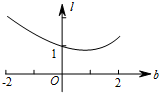 | B. |  | ||
| C. |  | D. | 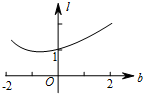 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
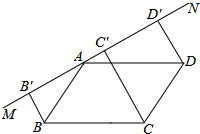 已知:如图,直线MN经过?ABCD的顶点A,BB′⊥MN,CC′⊥MN,DD′⊥MN,B′、C′、D′是垂足.
已知:如图,直线MN经过?ABCD的顶点A,BB′⊥MN,CC′⊥MN,DD′⊥MN,B′、C′、D′是垂足.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com