
【题目】某超市在“元旦”活动期间,推出如下购物优惠方案:
①一次性购物在![]() 元(不含
元(不含![]() 元)以内,不享受优惠;
元)以内,不享受优惠;
②一次性购物在![]() 元(含
元(含![]() 元)以上,
元)以上,![]() 元(不含
元(不含![]() 元)以内,一律享受九折优惠;
元)以内,一律享受九折优惠;
③一次性购物在![]() 元(含
元(含![]() 元)以上,一律享受八折优惠;
元)以上,一律享受八折优惠;
小敏在该超市两次购物分别付了90 元和270元,如果小敏把这两次购物改为一次性购物,则小敏至少需付款( )元
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
要求他一次性购买以上两次相同的商品,应付款多少元,就要先求出两次一共实际买了多少元,第一次购物有两种情况:①没有超过100元,即是90元;②刚好100,享受九折优惠,也是90元;第二次购物就只有一种情况,一种是超过100元但不超过350元一律9折;计算出他两次购物的实际款数,相加即是他应付款数,再根据优惠计算即可;
解:第一次购物可能有两种情况,这两种情况下付款方式不同(折扣率不同),
①没有超过100元,即是90元,则实际购物为90;
②一次性购物在![]() 元(含
元(含![]() 元)以上,
元)以上,![]() 元(不含
元(不含![]() 元)以内,享受九折优惠,设实际购物为x元,依题意得:x×0.9=90,
元)以内,享受九折优惠,设实际购物为x元,依题意得:x×0.9=90,
解得x=100元;
第二次购物消费270元,满足一次性购物在![]() 元(含
元(含![]() 元)以上,
元)以上,![]() 元(不含
元(不含![]() 元)以内,享受九折优惠;
元)以内,享受九折优惠;
设第二次实质购物价值为x元,那么依题意有x×0.9=270,
解得:x=300元;
∴他两次购物的实质价值为90+300=390或100+300=400,均超过了350元,因此均可以按照8折付款:
390×0.8=312(元),
400×0.8=320(元),
综上所述:如果小敏把这两次购物改为一次性购物,则小敏至少需付款312元;
故答案为:C.


科目:初中数学 来源: 题型:
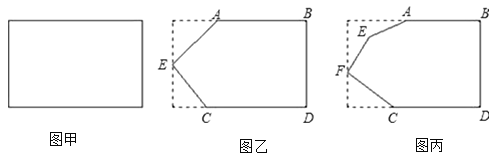
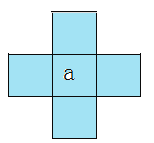
【题目】如图甲表示一个长方形纸片.
①如图乙,将图甲的一侧剪两刀后剪出3个角,那么AEC(________________);
②如图丙,将图甲的一侧剪三刀后剪出4个角,那么AEFC(________);
③按照上述剪法,将图甲的一侧剪出n个角,那么这n个角的和=(________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织七年级学生参加冬令营活动,本次冬令营活动分为甲、乙、丙三组进行.如图,条形统计图和扇形统计图反映了学生参加冬令营活动的报名情况,请你根据图中的信息回答下列问题:
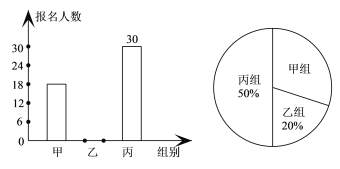
(1)七年级报名参加本次活动的总人数为 ,扇形统计图中,表示甲组部分的扇形的圆心角是 度;
(2)补全条形统计图;
(3)根据实际需要,将从甲组抽调部分学生到丙组,使丙组人数是甲组人数的3倍,则应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,乙团队人数不超过40人.设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.
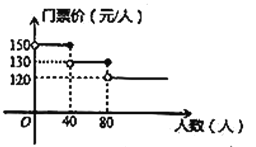
(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变
的函数关系式,并写出自变![]() 的取值范围;
的取值范围;
(2)若甲团队人数不超过80人,计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)端午节之后,该风景区对门票价格作了如下调整:人数不超过40人时,门票价格不变,人数超过40人但不超过80人时,每张门票降价![]() 元;人数超过80人时,每张门票降价
元;人数超过80人时,每张门票降价![]() 元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求
元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣8,﹣4),则点N的坐标为_____.
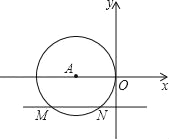
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:
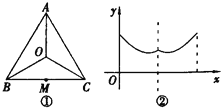
A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
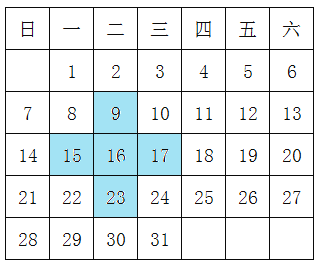
【题目】观察某月的月历,回答下列问题.
(1)设十字框中间的数为![]() ,求带阴影的十字框中间的5个数的和是多少?
,求带阴影的十字框中间的5个数的和是多少?
(2)小李一家外出游玩了5天,这5天的日期之和是75,小李一家是几号外出的?
(3)在该月的日历上用十字框框出5个数,能使这5个数的和为100吗?如果不能,请说明理由;如果能,请求出十字框中间的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
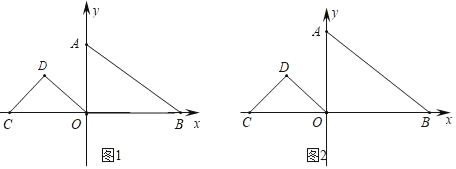
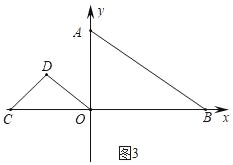
【题目】如图,已知在平面直角坐标系中,直线AB:![]() 与x轴、y轴分别交于B、A两点,等腰Rt△OCD,∠D=90°,C坐标为(﹣4,0).
与x轴、y轴分别交于B、A两点,等腰Rt△OCD,∠D=90°,C坐标为(﹣4,0).
(1)求A、B坐标;
(2)将△OCD沿x轴正方形平移,速度为1个单位为每秒,时间为t(0≤t≤6),设△OCD与△OAB重叠面积为S,请写出S与t之间的函数关系式;
(3)将△OCD绕O点旋转,当O、B、D三点构成的三角形为直角三角形时,请直接写出D点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com