练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距．人体构造学的研究成果表明，一般情况下人的指距d和身高h成如下所示的关系．

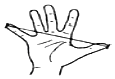
    指距d（cm）

    20

    21

    22

    23

    身高h（cm）

    160

    169

    178

    187

    （1）直接写出身高h与指距d的函数关系式；

    （2）姚明的身高是226厘米，可预测他的指距约为多少？（精确到0.1厘米）

    【答案】(1) h＝9d﹣20；(2) 姚明的身高是226厘米，可预测他的指距约为27.3厘米.

    【解析】

    （1）运用待定系数法求解即可；

    （2）把h＝226代入（1）中的结论即可．

    解：根据表格中数据，d每增加1，身高增加9cm，故d与h是一次函数关系，

    设这个一次函数的解析式是：h＝kd+b，

    ，

    解得，

    故一次函数的解析式是：h＝9d﹣20；

    （2）当h＝226时，9d﹣20＝226，解得d≈27.3．

    即姚明的身高是226厘米，可预测他的指距约为27.3厘米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在一次社会调查活动中，小李收集到某“健步走运动”团队20名成员一天行走的步数，记录如下：

    5640

    6430

    6520

    6798

    7325

    8430

    8215

    7453

    7446

    6754

    7638

    6834

    7326

    6830

    8648

    8753

    9450

    9865

    7290

    7850

    对这20个数据按组距1000进行分组，并统计整理．

    （1）请完成下面频数分布统计表；

    组别

    步数分组

    频数

    A

    5500≤x＜6500

    B

    6500≤x＜7500

    C

    7500≤x＜8500

    D

    8500≤x＜9500

    E

    9500≤x＜10500

    （2）在上图中请画出频数分布直方图；

    （3）若该团队共有200人，请估计其中一天行走步数少于8500步的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB = 6cm，∠CAB = 25°，P是线段AB上一动点，过点P作PM⊥AB交射线AC于点M，连接MB，过点P作PN⊥MB于点N．设A，P两点间的距离为xcm，P，N两点间的距离为ycm．（当点P与点A或点B重合时，y的值均为0）小海根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

    下面是小海的探究过程，请补充完整：

    （1）通过取点、画图、测量，得到了x与y的几组值，如下表：

    x/cm

    0.00

    0.60

    1.00

    1.51

    2.00

    2.75

    3.00

    3.50

    4.00

    4.29

    4.90

    5.50

    6.00

    y/cm

    0.00

    0.29

    0.47

    0.70

    1.20

    1.27

    1.37

    1.36

    1.30

    		<>1.00

    0.49

    0.00

    （说明：补全表格时相关数值保留两位小数）

    （2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

    （3）结合画出的函数图象，解决问题：当y=0.5时，与之对应的值的个数是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

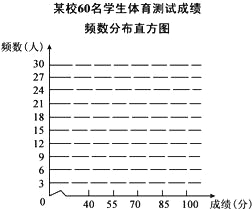
    【题目】某校为了更好的开展“学校特色体育教育”，从全校八年级的各班分别随机抽取了5名男生和5名女生，组成了一个容量为60的样本，进行各项体育项目的测试，了解他们的身体素质情况．下表是整理样本数据，得到的关于每个个体的测试成绩的部分统计表、图：某校60名学生体育测试成绩频数分布表

    成绩

    划记

    频数

    百分比

    优秀

    正正正

    a

    30%

    良好

    正正正正正正

    30

    b

    合格

    正

    9

    15%

    不合格

    3

    5%

    合计

    60

    60

    100%

    （说明：40﹣﹣﹣55分为不合格，55﹣﹣﹣70分为合格，70﹣﹣﹣85分为良好，85﹣﹣﹣100分为优秀）请根据以上信息，解答下列问题：

    （1）表中的a=_____，b=_____；

    （2）请根据频数分布表，画出相应的频数分布直方图；

    （3）如果该校八年级共有150名学生，根据以上数据，估计该校八年级学生身体素质良好及以上的人数为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

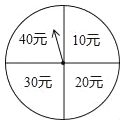
    【题目】端午节期间，扬州某商场为了吸引顾客，开展有奖促销活动，设立了一个可以自由转动的转盘，转盘被分成4个面积相等的扇形，四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样（如图）．规定：同一日内，顾客在本商场每消费满100元就可以转动转盘一次，商场根据转盘指针指向区域所标金额返还相应数额的购物券，某顾客当天消费240元，转了两次转盘．

    （1）该顾客最少可得 元购物券，最多可得 元购物券；

    （2）请用画树状图或列表的方法，求该顾客所获购物券金额不低于50元的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4，则以下四个结论中： ①△BDE是等边三角形； ②AE∥BC； ③△ADE的周长是9； ④∠ADE=∠BDC．其中正确的序号是（　　）

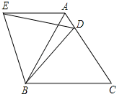
    A.②③④B.①②④C.①②③D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读并理解下面的证明过程，并在每步后的括号内填写该步推理的依据．如图，已知．求证：．

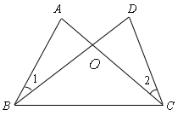
    证明：在△ABC和△DCB中，

    AB=DC(已知）

    AC=DB（已知）

    = （ ）

    ∴△ABC≌△DCB（ ）

    ∴∠ABC=∠DCB,∠ACB=∠DBC（ ）

    ∴∠ABC-∠DBC=∠DCB-∠ACB即∠1=∠2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对某个函数给定如下定义：若存在实数M>0，对于任意的函数值y，都满足|y|≤M，则称这个函数是有界函数．在所有满足条件的M中，其中最小值称为这个函数的边界值．现将有界函数y=2+1（0xm，1≤m≤2）的图象向下平移m个单位,得到的函数边界值是t，且≤t≤2，则m的取值范围是（ ）

    A. 1≤m≤ B. ≤m≤ C. ≤m≤ D. ≤m≤2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠BAC=90°，AB=3，AC=4，点D是BC的中点，将△ABD沿AD翻折得到△AED，连CE

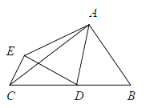
    （1）求证：AD=ED

    （2）连接BE，猜想△BEC的形状，并说明理由

    查看答案和解析>>

    同步练习册答案