
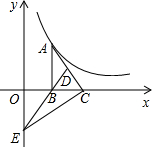
 如图,Rt△ABC的直角边BC在x轴正半轴上,点D为AC上一点,且AD=3DC,BD的反向延长线交y轴负半轴于E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BEC=6,则k=36.
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为AC上一点,且AD=3DC,BD的反向延长线交y轴负半轴于E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BEC=6,则k=36. 分析 连结OA、EA,如图,根据三角形面积公式,由AD=3DC得到S△ADE=3S△CDE,S△ADB=3S△CDB,则S△ABE=3S△BCE=18,再根据三角形面积公式得到S△ABE=SOAB=18,然后根据反比例函数的比例系数k的几何意义得到$\frac{1}{2}$×|k|=18,然后去绝对值即可得到满足条件的k的值.
解答 解: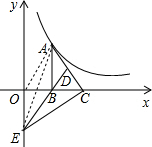 连结OA、EA,如图,
连结OA、EA,如图,
∵AD=3DC,
∴S△ADE=3S△CDE,S△ADB=3S△CDB,
即S△ABE+S△ADE=3(S△CDB+S△BCE),
∴S△ABE=3S△BCE=3×6=18,
∵OE∥AB,
∴S△ABE=SOAB=18,
∴$\frac{1}{2}$×|k|=18,
而k>0,
∴k=36.
故答案为36.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了三角形面积公式.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆顶端A的仰角为30°,向前走了10米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度不计).求旗杆AB的高度(精确到0.1米,已知$\sqrt{3}$≈1.73).
九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆顶端A的仰角为30°,向前走了10米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度不计).求旗杆AB的高度(精确到0.1米,已知$\sqrt{3}$≈1.73).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com