

���� ��1�����۵������ʿɵõ���ABD�ա�EDB����ô��ADB=��EBD������BF=DF��
��2����ͼ1�У��ɷ��ۿ�֪FBH=��HBC=��FHB����FB=FH����FB=FH=x����RT��AFB���ù��ɶ������ɣ�
������һ����ͼ2��BE=BH=BC=5ʱ����RT��ABH�У����AH���ɣ����ζ�����ͼ3�У�HE=BHʱ��ֻҪ֤����ABH�ա�DCH���ɣ�����������ͼ4�У�EB=EHʱ����RT��HCD�����ù��ɶ������ɣ�
��� ��1��֤�������۵�������֪��CD=ED��BE=BC
���ı���ABCD�Ǿ��Σ�
��AD=BC��AB=CD����BAD=90�㣬
��AB=DE��BE=AD��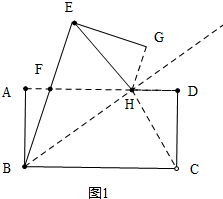
�ڡ�ABD���EDB�У�
$\left\{\begin{array}{l}{AB=DE}\\{BE=AD}\\{BD=BD}\end{array}\right.$��
���ABD�ա�EDB��SSS����
���EBD=��ADB��
��BF=DF��
��2������ͼ1�У��ߡ�GEH=��HCD=30�㣬��D=90�㣬DC=$\sqrt{3}$��
��DH=1��AH=AD-AD=5-1=4��
��AD��CB��
���FBH=��HBC=��FHB��
��FB=FH����FB=FH=x��
��RT��ABF����AB2+AF2=BF2��
�ࣨ$\sqrt{3}$��2+��4-x��2=x2��
��x=$\frac{19}{8}$��
������һ����ͼ2��BE=BH=BC=5ʱ��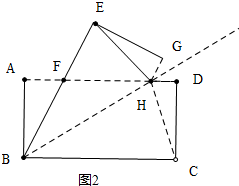
��RT��ABH����AB=$\sqrt{3}$��BH=5��
��AH=$\sqrt{B{H}^{2}-A{B}^{2}}$=$\sqrt{25-3}$=$\sqrt{22}$��
��DH=AD-AH=5-$\sqrt{22}$��
���ζ�����ͼ3�У�HE=BHʱ��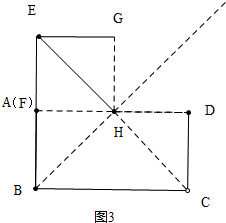
��EH=HC��
��HB=HC��
��RT��ABH��RT��DCH��
$\left\{\begin{array}{l}{HB=HC}\\{AB=DC}\end{array}\right.$
���ABH�ա�DCH��
��DH=AH=$\frac{1}{2}$AD=$\frac{5}{2}$��
����������ͼ4�У�EB=EHʱ��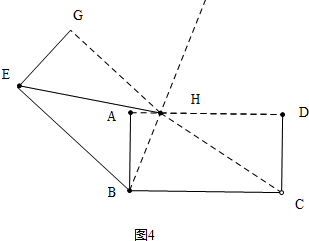
��EH=HC��
��HC=EB=BC=4��
��RT��HCD����HC=5��CD=$\sqrt{3}$��
��HD=$\sqrt{H{C}^{2}-C{D}^{2}}$=$\sqrt{22}$��
���� ���⿼����ε����ʡ����۲����ԣ�����Ĺؼ����������÷��۲����Խ�����⣬ѧ��������ۣ�ͨ��������Ŀ��ѵ����������Լ��Ĺ۲�����������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
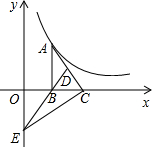 ��ͼ��Rt��ABC��ֱ�DZ�BC��x���������ϣ���DΪAC��һ�㣬��AD=3DC��BD�ķ����ӳ��߽�y�Ḻ������E��˫����y=$\frac{k}{x}$��k��0����ͼ����A����S��BEC=6����k=36��
��ͼ��Rt��ABC��ֱ�DZ�BC��x���������ϣ���DΪAC��һ�㣬��AD=3DC��BD�ķ����ӳ��߽�y�Ḻ������E��˫����y=$\frac{k}{x}$��k��0����ͼ����A����S��BEC=6����k=36���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0û�е��� | B�� | 0���෴����0 | C�� | 0�ľ���ֵ��0 | D�� | 0����С�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com