
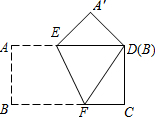
 把一张矩形纸片ABCD按如右图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,FC=2,则BF的长为4.
把一张矩形纸片ABCD按如右图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,FC=2,则BF的长为4.  小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:选择题
 “无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+2b)(a-b)=a2+ab-2b2 | D. | (a+b)2=a2+2ab+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
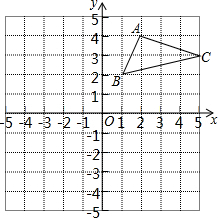 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
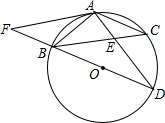 如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.
如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com