Question

5．如图，二次函数y=x²+bx+c的图象交x轴于A（-1，0）、B（3，0）两点，交y轴于点C，连接BC，动点P以每秒1个单位长度的速度从A向B运动，动点Q以每秒$\sqrt{2}$个单位长度的速度从B向C运动，P、Q同时出发，连接PQ，当点Q到达C点时，P、Q同时停止运动，设运动时间为t秒．

（1）求二次函数的解析式； 
（2）如图1，当△BPQ为直角三角形时，求t的值；
（3）如图2，当t＜2时，延长QP交y轴于点M，在抛物线上存在一点N，使得PQ的中点恰为MN的中点，请直接写出N点的坐标．

Answer 1

分析 （1）根据待定系数法，可得函数解析式；
（2）首先根据待定系数法，求出BC所在的直线的解析式，再分别求出点P、点Q的坐标各是多少；然后分两种情况：①当∠QPB=90°时；②当∠PQB=90°时；根据等腰直角三角形的性质，求出t的值各是多少即可．
（3）首先延长MQ交抛物线于点N，H是PQ的中点，再用待定系数法，求出PQ所在的直线的解析式，然后根据PQ的中点恰为MN的中点，判断出是否存在满足题意的点N即可．

解答 解：（1）∵二次函数y=x²+bx+c的图象经过A（-1，0）、B（3，0）两点，
∴$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$，
∴二次函数的表达式是：y=x²-2x-3．
（2）∵y=x²-2x-3，
∴点C的坐标是（0，-3），
①如图1：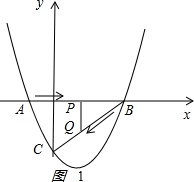
，
当∠QPB=90°时，
∵经过t秒，AP=t，BQ=$\sqrt{2}$t，BP=3-（t-1）=4-t．
∵OB=OC=3，
∴∠OBC=∠OCB=45°．
∴BQ=$\sqrt{2}$BP
∴$\sqrt{2}$t=$\sqrt{2}$×（4-t）
解得t=2．
即当t=2时，△BPQ为直角三角形．
②如图2：
，
当∠PQB=90°时，
∵∠PBQ=45°，
∴BP=$\sqrt{2}$BQ．
∵BP═4-t，BQ=$\sqrt{2}$t，
∴4-t=$\sqrt{2}$×$\sqrt{2}$t
解得t=$\frac{4}{3}$
即当t=$\frac{4}{3}$时，△BPQ为直角三角形．
综上，当△BPQ为直角三角形，t=2或$\frac{4}{3}$．
（3）N点的坐标是（2，-3）
（3）如图3：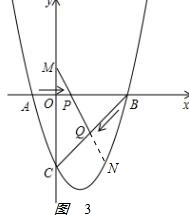
，
延长MQ交抛物线于点N，H是PQ的中点，
设PQ所在的直线的解析式是y=px+q，
∵点P的坐标是（t-1，0），点Q的坐标是（3-t，-t），
$\left\{\begin{array}{l}{p（t-1）+q=0}\\{p（3-t）+q=-t}\end{array}\right.$
解得$\left\{\begin{array}{l}{p=\frac{t}{2t-4}}\\{q=\frac{t-{t}^{2}}{4-2t}}\end{array}\right.$．
∴PQ所在的直线的解析式是y=$\frac{t}{2t-4}$x+$\frac{t-{t}^{2}}{4-2t}$，
∴点M的坐标是（0，$\frac{t-{t}^{2}}{4-2t}$）．
∵$\frac{t-1+3-t}{2}$=1，$\frac{-t+0}{2}$=-$\frac{t}{2}$，
∴PQ的中点H的坐标是（1，-$\frac{t}{2}$）
假设PQ的中点恰为MN的中点，
∵1×2-0=2，$\frac{t}{2}$×2-$\frac{t-{t}^{2}}{4-2t}$=$\frac{3{t}^{2}-5t}{4-2t}$，
∴点N的坐标是（2，$\frac{3{t}^{2}-5t}{4-2t}$），
又∵点N在抛物线上，
∴$\frac{3{t}^{2}-5t}{4-2t}$=2²-2×2-3=-3，
∴点N的坐标是（2，-3），
解得t=$\frac{9+\sqrt{33}}{2}$或t=$\frac{9-\sqrt{33}}{2}$，
∵t＜2，
∴t=$\frac{9-\sqrt{33}}{2}$，
∴当t＜2时，延长QP交y轴于点M，当t=$\frac{9-\sqrt{33}}{2}$时在抛物线上存在一点N（2，-3），使得PQ的中点恰为MN的中点．

点评 本题考查了二次函数综合题，（1）此题主要考查了二次函数综合题，考查了分析推理能力，考查了分类讨论思想的应用，考查了数形结合思想的应用，考查了从已知函数图象中获取信息，并能利用获取的信息解答相应的问题的能力；（2）此题还考查了等腰三角形的性质和应用，考查了分类讨论思想的应用，要熟练掌握，解答此题的关键是要明确：①等腰三角形的两腰相等．②等腰三角形的两个底角相等．③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合；（3）此题还考查了待定系数法求函数解析式的方法，要熟练掌握．