练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

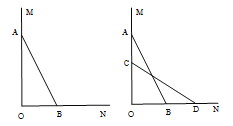
    【题目】（本题6分）如图，一架2.5米长的梯子AB，斜靠在一竖直的墙AO上，这时梯足B到墙底端O的距离为0.7米, 如果梯子的顶端沿墙下滑0.4米，那么梯足将向外移多少米？

    【答案】0.8米

    【解析】

    试题首先根据Rt△AOB的勾股定理求出AO的长度，然后计算出OC的长度，根据Rt△COD的勾股定理求出OD的长度，最后根据BD=OD－0B进行求解.

    试题解析：由题意，在Rt△AOB中，AB=2.5米，BO=0.7米

    由勾股定理得AO==2.4米

    ∴CO=AO－AC=2.4－0.4=2米

    在Rt△COD中，CD=2.5米，CO=2米 由勾股定理得OD==1.5米

    ∴BD=OD-OB=1.5－0.7=0.8米

    答：梯足将向外移0.8米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩．她从中随机调查了若干名女生的测试成绩（单位：米），并将统计结果绘制成了如下的统计图表（内容不完整）．

    测试成绩

    合计

    频数

    3

    27

    9

    m

    1

    n


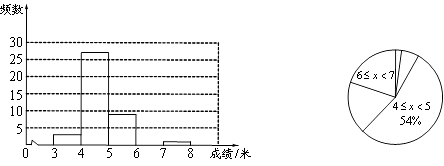
    请你结合图表中所提供的信息，回答下列问题：
    （1）表中m= ， n=；
    （2）请补全频数分布直方图；
    （3）在扇形统计图中， 这一组所占圆心角的度数为度；
    （4）如果掷实心球的成绩达到6米或6米以上为优秀，请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在平行四边形ABCD中，E，F是对角线BD上的两点，且BF＝DE．

    求证：（1）AE＝CF；

    （2）四边形AECF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒，已知购买一个台灯比购买一个手电筒多用20元，若用400元购买台灯和用160元购买手电筒，则购买台灯的个数是购买手电筒个数的一半．

    （1）求购买该品牌一个台灯、一个手电筒各需要多少元？

    （2）经商谈，商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠，如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个，且该公司购买台灯和手电筒的总费用不超过670元，那么荣庆公司最多可购买多少个该品牌台灯？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD中，AB⊥AC，AB=2，AC=4．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转α°，分别交直线BC、AD于点E、F．

    （1）当α=　 　°，四边形ABEF是平行四边形；

    （2）在旋转的过程中，从A、B、C、D、E、F中任意4个点为顶点构造四边形．

    ①α=　 　°，构造的四边形是菱形；

    ②若构造的四边形是矩形，求出该矩形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小凡与小光从学校出发到距学校5千米的图书馆看书，小光直接去图书馆, 小凡途中从路边超市买了一些学习用品，如图反应了他们俩人离开学校的路程s（千米）与时间t（分钟）的关系，请根据图象提供的信息回答问题：

    （1） 是描述小凡的运动过程（填或）；

    （2）小凡和小光先出发的是 ，先出发了 分钟；

    （3）小凡与小光先到达图书馆的是 ，先到了 分钟；

    （4）求小凡与小光从学校到图书馆的平均速度各是多少？（不包括中间停留的时间）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的袋子中装有若干个除颜色外均相同的小球，小明每次从袋子中摸出一个球，记录下颜色，然后放回，重复这样的试验1000次，记录结果如下：

    实验次数n

    200

    300

    400

    500

    600

    700

    800

    1000

    摸到红球次数m

    151

    221

    289

    358

    429

    497

    568

    701

    摸到红球频率

    0.75

    0.74

    0.72

    0.72

    0.72

    0.71

    a

    b

    （1）表格中a=________，b=_________；

    （2）估计从袋子中摸出一个球恰好是红球的概率约为________；（精确到0.1）

    （3）如果袋子中有14个红球，那么袋子中除了红球，还有多少个其他颜色的球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，图中的小方格都是边长为1的正方形，△ABC的A，B，C三点坐标为A（2,0）、B（2,2）、C（6，3）。

    （1）请在图中画出一个△ ,使△ 与△ABC是以坐标原点为位似中心，相似比为2的位似图形。
    （2）求△ 的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．

    （1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；

    （2）设∠BAC= ，∠DCE= ．

    ① 如图2，当点D在线段CB上，∠BAC≠90°时，请你探究与之间的数量关系，并证明你的结论；

    ② 如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时与之间的数量关系（不需证明）．

    查看答案和解析>>

    同步练习册答案