
【题目】解下列关于x或y的方程。
![]()
![]()
![]()
![]()
【答案】(1) ![]() ;
;
(2)当b=0时,方程没有实数根;当b≠0时,![]() ;
;
(3)![]() ;
;
(4) 当b<0时,方程没有实数根;当b>0时,![]() .
.
【解析】
(1)把a看作已知数,按照移项合并同类项、系数化为1即可求得;
(2)把b看作已知数,按照去括号、移项、系数化为1即可求得.注意对b值的范围进行分类讨论;
(3)把a看作已知数,按照合并同类项、系数化为1,再开方即可求得;
(4)把b看作已知数,按照移项合并同类项、系数化为1,再开方即可求得.注意对b值的范围进行分类讨论;
解:(1)合并同类项得![]()
系数化为1得![]()
(2)去括号得![]()
移项得![]()
当b=0时,方程没有实数根;
当b≠0时,系数化为1得![]() .
.
(3)合并同类项得![]()
系数化为1得![]()
∴方程的根是![]()
(4)移项合并同类项得![]()
∵b≠0
∴系数化为1得![]()
当b<0时,方程没有实数根;
当b>0时,![]()


科目:初中数学 来源: 题型:
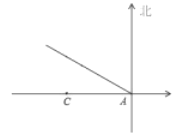
【题目】一船在灯塔![]() 的正东方向
的正东方向![]() 海里的
海里的![]() 处,以20海里/时的速度沿北偏西
处,以20海里/时的速度沿北偏西![]() 方向航行。
方向航行。
(1)多长时间后,船距灯塔最近?
(2)多长时间后,船到灯塔的正北方向?此时船距灯塔有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,![]() 三点在同一直线上,
三点在同一直线上,![]() .
.
(1)已知点![]() 在直线
在直线![]() 上,根据条件,请补充完整图形,并求
上,根据条件,请补充完整图形,并求![]() 的长;
的长;
![]()
(2)已知点![]() 在直线
在直线![]() 上,
上,![]() 分别是
分别是![]() ,
,![]() 的中点,根据条件,请补充完整图形,并求
的中点,根据条件,请补充完整图形,并求![]() 的长,直接写出
的长,直接写出![]() 与
与![]() 的长存在的数量关系;
的长存在的数量关系;
![]()
(3)已知点![]() 在直线
在直线![]() 上,
上,![]() 分别是
分别是![]() ,
,![]() 的中点,根据条件,请补充完整图形,并求
的中点,根据条件,请补充完整图形,并求![]() 的长,直接写出
的长,直接写出![]() 与
与![]() 的长存在的数量关系.
的长存在的数量关系.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
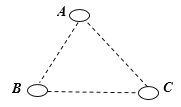
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC上一点,BE![]() BC,连接AE,作BF⊥AE,分别与AE、CD交于点K、F,G、H分别在AD、AE上,且四边形KFGH是矩形,则
BC,连接AE,作BF⊥AE,分别与AE、CD交于点K、F,G、H分别在AD、AE上,且四边形KFGH是矩形,则![]() ________.
________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)(-12.5)+20.5;
(2)2![]() ×(-
×(-![]() );
);
(3)10+2÷![]() ×(-2);
×(-2);
(4)1-(1-0.5)×![]() ×[2-(-2)2];
×[2-(-2)2];
(5)-52+(-2)÷![]() 2;
2;
(6)-22÷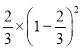 ;
;
(7)17-23÷(-2)×3;
(8)2×(-5)+23-3÷![]() ;
;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国的茶文化源远流长,根据制作方法和茶多酚氧化(发酵)程度的不同,可分为六大类:绿茶(不发酵)、白茶(轻微发酵)、黄茶(轻发酵)、青茶(半发酵)、黑茶(后发酵)、红茶(全发酵).春节将至,为款待亲朋好友,小叶去茶庄选购茶叶.茶庄有碧螺春、龙井两种绿茶,一种青茶——武夷岩茶及一种黄茶——银针出售.
(1)随机购买一种茶叶,是绿茶的概率为________;
(2)随机购买两种茶叶,求一种是绿茶、一种是银针的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”的
对于图形![]() 和图形
和图形![]() ,若图形
,若图形![]() 和图形
和图形![]() 分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形
分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形![]() 和图形
和图形![]() 是“中心轴对称”的。
是“中心轴对称”的。
特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的。
(1)如图1,在正方形ABCD中,点![]() ,点
,点![]() ,
,
①下列四个点![]() ,
,![]() ,
,![]() ,
,![]() 中,与点A是“中心轴对称”的是________;
中,与点A是“中心轴对称”的是________;
②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标![]() 的取值范围;
的取值范围;
(2)四边形GHJK的四个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,一次函数
,一次函数![]() 图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。
图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com