
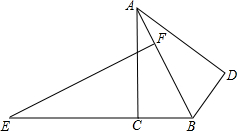
 如图,直角三角形ABC中,∠ACB=90°,BC=3,AC=6,E为BC延长线上一点,且EC=$\frac{25}{4}$,过点E作EF⊥AB交AB于F,将△ABC沿AB翻折,得到△ABD,将△ABD绕点B旋转,在旋转过程中,记旋转中△ABD为△A′B′D′.设直线A′D′与射线EF交于点M,与射线EB交于点N,当△EMN是以∠MEN为底角的等腰三角形时,EN=13或$\frac{37}{4}$+3$\sqrt{5}$.
如图,直角三角形ABC中,∠ACB=90°,BC=3,AC=6,E为BC延长线上一点,且EC=$\frac{25}{4}$,过点E作EF⊥AB交AB于F,将△ABC沿AB翻折,得到△ABD,将△ABD绕点B旋转,在旋转过程中,记旋转中△ABD为△A′B′D′.设直线A′D′与射线EF交于点M,与射线EB交于点N,当△EMN是以∠MEN为底角的等腰三角形时,EN=13或$\frac{37}{4}$+3$\sqrt{5}$. 分析 情形1:如图1中,当∠BEF=∠NME时,易证BN=NA′,设BN=NA′=x,在RT△BND′利用勾股定理即可解决问题.情形2:如图2中,当∠MEN=∠MNE时,证明BN=BA′即可解决问题.
解答 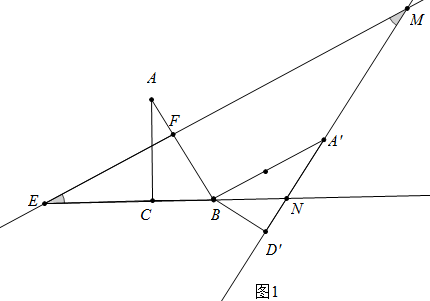 解:如图1中,当∠BEF=∠NME时,
解:如图1中,当∠BEF=∠NME时,
∵∠BEF+∠ABC=90°,∠A+∠ABC=90°,
∴∠BEF=∠A=∠BA′D′=∠NME,
∴BA′∥EM,
∴∠NBA′=∠BEF=∠BA′N,
∴NB=NA′,设BN=NA′=x,
在RT△BND′中,∵BD′2+ND′2=BN2,
∴32+(6-x)2=x2,
x=$\frac{15}{4}$,
∴EN=EB+BN=EC+BC+BN=$\frac{25}{4}$+3+$\frac{15}{4}$=13,
如图2中,当∠MEN=∠MNE时,
∵∠MEN=∠BAC=∠BA′N=∠A′NE, ∴BA′=BN=AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
∴BA′=BN=AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
∴EN=EC+BC+BN=$\frac{25}{4}$+3=3$\sqrt{5}$=$\frac{37}{4}$+3$\sqrt{5}$.
故答案为13或$\frac{37}{4}$+3$\sqrt{5}$.
点评 本题考查旋转的性质、勾股定理、平行线的性质等知识,解题的关键是正确画出图形,学会分类讨论的思想,小心漏解,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2{a^2}}$ | D. | $\sqrt{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
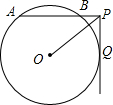 如图,⊙O中,点P是弦AB延长线上的一点,连接OP,过P作PQ⊥AP,且与⊙O相切于Q,若OP=4,∠APO=30°,则PA的长是( )
如图,⊙O中,点P是弦AB延长线上的一点,连接OP,过P作PQ⊥AP,且与⊙O相切于Q,若OP=4,∠APO=30°,则PA的长是( )| A. | 2$\sqrt{3}$+2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{13}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
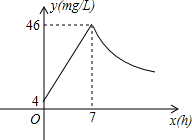 近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如下图,根据题中相关信息回答下列问题:
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如下图,根据题中相关信息回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com