练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．若2a2-a-3=0，则5+2a-4a2=-1．

    分析 已知等式变形求出2a2-a的值，原式变形后代入计算即可求出值．

    解答 解：∵2a2-a-3=0，
    ∴2a2-a=3，
    则原式=5-2（2a2-a）=5-6=-1，
    故答案为：-1．

    点评 此题考查了代数式求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    10．比较大小：$|{-1\frac{3}{4}}|$＜-（-1.8）（填“＞”、“＜”或“=”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．实验探究：
    （1）动手操作：
    ①如图1，将一块直角三角板DEF放置在直角三角板ABC上，使三角板DEF的两条直角边DE、DF分别经过点B、C，且BC∥EF，已知∠A=30°，则∠ABD+∠ACD=60°；
    ②如图2，若直角三角板ABC不动，改变等腰直角三角板DEF的位置，使三角板DEF的两条直角边DE、DF仍然分别经过点B、C，那么∠ABD+∠ACD=60°；

    （2）猜想证明：
    如图3，∠BDC与∠A、∠B、∠C之间存在着什么关系，并说明理由；
    （3）灵活应用：
    请你直接利用以上结论，解决以下列问题：
    ①如图4，BE平分∠ABD，CE平分∠ACD，若∠BAC=40°，∠BDC=120°，求∠BEC的度数；
    ②如图5，∠ABD，∠ACD的10等分线相交于点F1、F2、…、F9，
    若∠BDC=120°，∠BF3C=64°，则∠A的度数为40°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．二次函数的部分对应值如下表：
    x…-3-20135…
    y…70-8-957…
    由图可知该二次函数的图象对称轴为x=1，x=2对应的函数值y=-8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

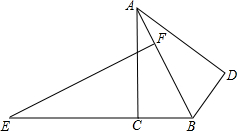    15．如图，直角三角形ABC中，∠ACB=90°，BC=3，AC=6，E为BC延长线上一点，且EC=$\frac{25}{4}$，过点E作EF⊥AB交AB于F，将△ABC沿AB翻折，得到△ABD，将△ABD绕点B旋转，在旋转过程中，记旋转中△ABD为△A′B′D′．设直线A′D′与射线EF交于点M，与射线EB交于点N，当△EMN是以∠MEN为底角的等腰三角形时，EN=13或$\frac{37}{4}$+3$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．平行四边形ABCD的周长是56cm，对角线相交于点O，△BOC的周长比△AOB的周长小8cm，则AB=18cm，BC=10cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．在Rt△ABC中，∠C=90°，∠A=30°，AB=4，则AC=2$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．小明家、学校与图书馆依次在一条直线上，小明、小亮两人同时分别从小明家和学校出发沿直线匀速步行到图书馆借阅图书，小明到达图书馆花了20分钟，小亮每分钟步行40米，小明离学校的距离y（米）与两人出发时间x（分）之间的函数图象如图所示．
    （1）小明每分钟步行60米，a=960，小明家离图书馆的距离为1200米．
    （2）在图中画出小亮离学校的距离y（米）与x（分）之间的函数图象．
    （3）求小明和小亮在途中相遇时二人离图书馆的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．计算$\sqrt{12}×\sqrt{\frac{1}{3}}+\sqrt{5}×\sqrt{3}$的结果在（　　）
    A．4至5之间B．5至6之间C．6至7之间D．7至8之间

    查看答案和解析>>

    同步练习册答案