
分析 直接利用反比例函数的性质写出答案即可.
解答 解:函数y=-$\frac{3}{2x}$的图象叫双曲线,它位于第二、四象限,在每一个象限内,y随x的增大而增大.
∵点(a,3)在该图象上,
∴-$\frac{3}{2a}$=3,
则a=-$\frac{1}{2}$;
若(b,-6b)在该图象上,
-$\frac{3}{2b}$=-6b,
则b=±$\frac{1}{2}$.
故答案为:双曲线,二、四,增大,-$\frac{1}{2}$,±$\frac{1}{2}$.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k≠0)图象上点的横纵坐标之积为k.也考查了反比例函数的性质.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
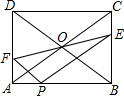 如图,矩形ABCD中,对角线AC,BD相交于点O,AB=4,BC=3,在线段AB上取一点P,过点P作AC的平行线交BC于点E,连结EO并延长交AD于点F,连接PF.
如图,矩形ABCD中,对角线AC,BD相交于点O,AB=4,BC=3,在线段AB上取一点P,过点P作AC的平行线交BC于点E,连结EO并延长交AD于点F,连接PF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com