
| p |
| p |
| p |
| 3 |
| 3 |
| p |
| p |
|
|
|
| 3 |
| 3 |
|
| 3 |
| a |
| 3 |
| a |
|
| 1 |
| a |
| 1 |
| a |
|
|
|
| 3 |
| 3 |
|
| 3 |
| a |
| 3 |
| a |
|
| 1 |
| a |
| 1 |
| a |
| 3 |
| a |
| 1 |
| a |


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
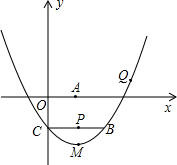 如图,过点C(0,-2)的抛物线y=ax2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴交抛物线于点B,点P在线段BC上,CP=m.
如图,过点C(0,-2)的抛物线y=ax2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴交抛物线于点B,点P在线段BC上,CP=m.查看答案和解析>>
科目:初中数学 来源: 题型:
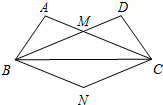 如图,在△ABC和△DCB中,AC=BD,AB=CD,AC、BD交于点M.
如图,在△ABC和△DCB中,AC=BD,AB=CD,AC、BD交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:
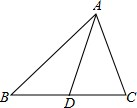 已知:如图△ABC中AD是BC的中线,AB=5cm,AC=3cm,则△ABD和△ACD的周长的差为
已知:如图△ABC中AD是BC的中线,AB=5cm,AC=3cm,则△ABD和△ACD的周长的差为查看答案和解析>>
科目:初中数学 来源: 题型:
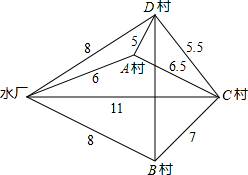 如图,为解决A、B、C、D四个村庄的用水问题,决定在已建水厂与这四个村庄之间铺设供水管道.现在已知这四个村庄及水厂之间的距离(千米).由于地质构造不一样,经测算,在A村和D村之间铺设水管的费用要比其他地方铺设水管的费用每千米增加150%.问:能把水输送到这四个村庄的输水管道成本最省的一条线路的长度是
如图,为解决A、B、C、D四个村庄的用水问题,决定在已建水厂与这四个村庄之间铺设供水管道.现在已知这四个村庄及水厂之间的距离(千米).由于地质构造不一样,经测算,在A村和D村之间铺设水管的费用要比其他地方铺设水管的费用每千米增加150%.问:能把水输送到这四个村庄的输水管道成本最省的一条线路的长度是查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com