
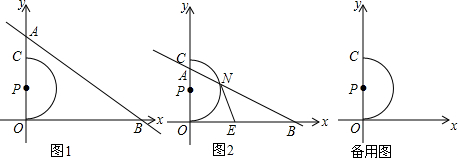
分析 (1)首先求出直线与x轴交点坐标,进而得出答案,再利用锐角三角函数关系得出∠ABO的度数;
(2)①分别利用∠NEB=90°和∠ENB=90°,结合切线的性质得出m的值;
②首先求出NG:EN=$\sqrt{15}:4$,再得出△PHN∽△NGE,再利用相似三角形的性质,进而得出m的值.
解答 解:(1)当y=0,则0=-$\frac{{\sqrt{3}}}{3}$x+m,
解得:x=$\sqrt{3}$m,
故B点坐标是$(\sqrt{3}m,0)$(用含m的代数式表示),
∵一次函数y=-$\frac{{\sqrt{3}}}{3}$x+m与y轴交于点(0,m),
∴tan∠ABO=$\frac{m}{\sqrt{3}m}$=$\frac{\sqrt{3}}{3}$,
∴∠ABO=30°;
故答案为:($\sqrt{3}$m,0),30;
(2)①如图①,假设存在这样的m的值,使得△EBN是直角三角形.连接NP
若∠NEB=90°,∵NE是⊙P的切线,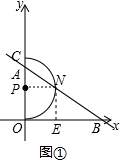
∴∠PNE=90°,
∵∠POE=90°,
∴四边形OPNE是矩形,
∴PN=2,∠APN=90°,
在Rt△APN中,PN=2,∠BAO=60°,
∴PA=$\frac{2\sqrt{3}}{3}$,
∴m=2+$\frac{2\sqrt{3}}{3}$,
若∠ENB=90°,∵NE是⊙P的切线,
∴∠PNE=90°,
∴点P、N、B三点共线,即点P与点A重合,
∴m=2,
综上可知,m=2或2+$\frac{2\sqrt{3}}{3}$;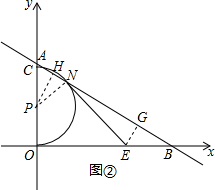
②如图②,连接PN,过点E作,EG⊥AB于G,过点P作,PH⊥AB于H,
则PA=m-2,PH=$\frac{{\sqrt{3}}}{2}(m-2)$,
∵$\frac{EB}{EO}$=$\frac{1}{2}$,∴EB=$\frac{{\sqrt{3}}}{3}m$,EN=EO=$\frac{{2\sqrt{3}}}{3}m$,EG=$\frac{1}{2}EB=\frac{{\sqrt{3}}}{6}m$,
∴EG:EN=1:4,∴NG:EN=$\sqrt{15}:4$,
∵∠PNE=90°,∴∠PNH+∠ENG=90°,
∵∠GNE+∠NEG=90°,
∴∠NEG=∠PNH,
∵∠PHN=∠EGN=90°,
∴△PHN∽△NGE,
∴$\frac{NG}{EN}$=$\frac{PH}{PN}$,
∴$\frac{\frac{\sqrt{3}}{2}(m-2)}{2}$=$\frac{\sqrt{15}}{4}$,
解得:m=$2+\sqrt{5}$.
点评 此题主要考查了圆的综合以及相似三角形的判定与性质和切线的性质等知识,熟练应用相似三角形的判定与性质是解题关键.


科目:初中数学 来源: 题型:选择题
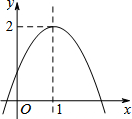 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
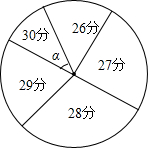 某校组织了九年级学生英语口语模拟测试,现从中随机抽取部分学生的口语模拟测试成绩统计如下.
某校组织了九年级学生英语口语模拟测试,现从中随机抽取部分学生的口语模拟测试成绩统计如下.| 口语成绩(分) | 人数(人) | 百分比(%) |
| 26 | 8 | 16 |
| 27 | 24 | |
| 28 | 15 | |
| 29 | m | |
| 30 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当x>1时,y随x的增大而减小 | B. | 图象与y轴的交点坐标为(0,2) | ||
| C. | 图象的开口向上 | D. | 图象的顶点坐标是(-1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com