练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线C1的解析式为y= -x2+bx+c，C1经过A（-2,5）、B（1,2）两点.

    （1）求b、c的值；

    （2）若一条抛物线与抛物线C1都经过A、B两点，且开口方向相同，称两抛物线是“兄弟抛物线”，请直接写出C1的一条“兄弟抛物线”的解析式.

    【答案】（1）b=-2，c=5；（2）(答案不唯一).

    【解析】

    （1）直接把点代入，求出的值即可得出抛物线的解析式；

    （2）根据题意，设“兄弟抛物线”的解析式为：，直接把点代入即可求得答案.

    （1）∵在C1上 ，

    ∴ ，

    解得： .

    （2）根据“兄弟抛物线”的定义，知：“兄弟抛物线”经过A（-2,5）、B（1,2）两点，且开口方向相同，

    ∴设“兄弟抛物线”的解析式为：，

    ∵在“兄弟抛物线”上，

    ∴ ，

    解得：.

    ∴另一条“兄弟抛物线”的解析式为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

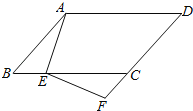
    【题目】如图，在平行四边形ABCD中，点E在BC边上，点F在DC的延长线上，且∠DAE＝∠F．

    （1）求证：△ABE∽△ECF；

    （2）若AB＝5，AD＝8，BE＝2，求FD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

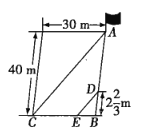
    【题目】如图，在一个长40m，宽30m的长方形小操场上，王刚从A点出发，沿着A→B→C的路线以3m/s的速度跑向C地.当他出发4s后，张华有东西需要交给他，就从A地出发沿王刚走的路线追赶，当张华跑到距B地m的D处时，他和王刚在阳光下的影子恰好重叠在同一条直线上.此时，A处的小旗在阳光下的影子也恰好落在对角线AC上.求：

    （1）他们的影子重叠时，两人相距多少米（DE的长）？

    （2）张华追赶王刚的速度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，点是中点.连接.作，垂足为，的外接圆交于点，连接.

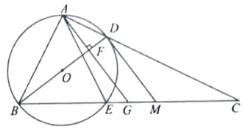
    （1）求证：；

    （2）过点作圆的切线，交于点.若，求的值；

    （3）在（2）的条件下，当时，求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据全等形的定义，我们把四个角分别相等，四条边分别相等的两个凸四边形叫做全等四边形．

    （1）某同学在探究全等四边形的判定时，得到如下三个命题，请判断它们是否正确（直接在横线上填写“真”或“假”）．

    ①四条边成比例的两个凸四边形全等；（　 　命题）

    ②四个角分别相等的两个凸四边形全等；（　 　命题）

    ③两个面积相等的正方形全等；（　 　命题）

    ④三角分别相等，且其中两角夹边相等两个凸四边形全等．（　 　命题）

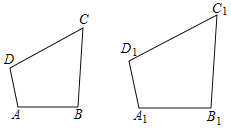
    （2）如图，在四边形ABCD和四边形A1B1C1D1中，∠ABC＝∠A1B1C1，∠BCD＝∠B1C1D1，AB＝A1B1，BC＝∠B1C1，CD＝C1D1．求证：在四边形ABCD和四边形A1B1C1D1全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

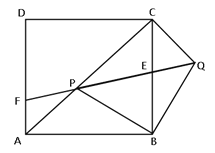
    【题目】如图，等腰Rt△BPQ的顶点P在正方形ABCD的对角线AC上（P与AC不重合），∠PBQ=90°，QP与BC交于E,QP延长线交AD于F，连CQ.

    (1)①求证：AP=CQ ；

    ②求证：

    (2)当时，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．

    （1）求y与x之间的函数关系式；

    （2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？

    （3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.

    (1)试求y与x之间的函数关系式;

    (2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

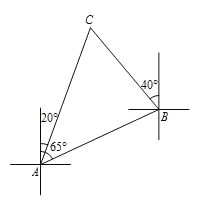
    【题目】如图，一艘船由A港沿北偏东65°方向航行km至B港，然后再沿北偏西40°方向航行至C港，C港在A港北偏东20°方向.

    求：（1）∠C的度数；

    （2）A，C两港之间的距离为多少km.

    查看答案和解析>>

    同步练习册答案