
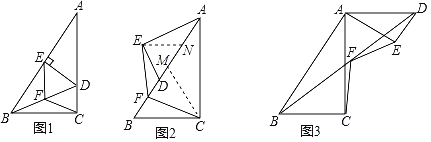
【题目】如图1,△ABC是直角三角形,∠ACB=90°,点D在AC上,DE⊥AB于E,连接BD,点F是BD的中点,连接EF,CF.
(1)EF和CF的数量关系为 ;
(2)如图2,若△ADE绕着点A旋转,当点D落在AB上时,小明通过作△ABC和△ADE斜边上的中线CM和EN,再利用全等三角形的判定,得到了EF和CF的数量关系,请写出此时EF和CF的数量关系 ;
(3)若△AED继续绕着点A旋转到图3的位置时,EF和CF的数量关系是什么?写出你的猜想,并给予证明.
【答案】(1)EF=CF;(2)EF=CF;(3)EF=CF,证明详见解析.
【解析】
(1)根据DE⊥AB,可得∠ACB=∠DEB=90°,再根据中点平分线段长度可得EF=CF=![]() BD,即可证明EF=CF;
BD,即可证明EF=CF;
(2)根据三角形斜边中线定理可得CM=BM=AM=![]() AB,AN=EN=DN=
AB,AN=EN=DN=![]() AD,即可推出FM=EN,再根据旋转的性质得ENF=∠CMF,即可证明△EFN≌△FCM(SAS),得证EF=CF;
AD,即可推出FM=EN,再根据旋转的性质得ENF=∠CMF,即可证明△EFN≌△FCM(SAS),得证EF=CF;
(3)取AB的中点M,AD的中点N,连接MC,MF,EN,FN,通过证明四边形MFNA是平行四边形,可得NF=AM,∠FMA=∠ANF,再通过三角形斜边中线定理和角的和差关系可得CM=NF,即可证明△MFC≌△NEF(SAS),从而得证FE=FC.
解:(1)EF=CF,
理由:∵DE⊥AB,
∴∠ACB=∠DEB=90°,
∵F是BD的中点,
∴EF=CF=![]() BD;
BD;
故答案为:EF=CF;
(2)EF=CF,
理由:∵∠AED=∠ACB=90°,CM和EN是△ABC和△ADE斜边上的中线,
∴CM=BM=AM=![]() AB,AN=EN=DN=
AB,AN=EN=DN=![]() AD,
AD,
∵点F是BD的中点,
∴BF=FD,
∴AN+BF=DN+DF=FN=![]() AB,
AB,
∴FN=CM=AM,
∵FM=FN﹣MN,AN=AM﹣MN,
∴FM=AN,
∴FM=EN,
∵△ADE绕着点A旋转,当点D落在AB上,
∴∠EAD=∠CAB,
∵∠EAN=∠AEN,∠MAC=∠ACM,
∴∠ENF=∠EAN+∠AEN=2∠EAN,∠CMF=∠CAM+∠ACM=2∠CAM,
∴∠ENF=∠CMF,
在△EFN与△FCM中,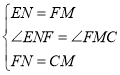 ,
,
∴△EFN≌△FCM(SAS),
∴EF=CF;
故答案为:EF=CF;
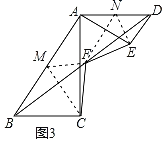
(3)猜想,EF=CF,
理由:如图3中,取AB的中点M,AD的中点N,连接MC,MF,EN,FN.
∵BM=MA,BF=FD,
∴MF∥AD,MF=![]() AD,
AD,
∵AN=ND,
∴MF=AN,MF∥AN,
∴四边形MFNA是平行四边形,
∴NF=AM,∠FMA=∠ANF,
在Rt△ADE中,∵AN=ND,∠AED=90°,
∴EN=![]() AD=AN=ND,同理CM=
AD=AN=ND,同理CM=![]() AB=AM=MB,
AB=AM=MB,
在△AEN和△ACM中,
∠AEN=∠EAN,∠MCA=∠MAC,
∵∠MAC=∠EAN,
∴∠AMC=∠ANE,
又∵∠FMA=∠ANF,
∴∠ENF=∠FMC,
∵AM=FN,AM=CM,
∴CM=NF,
在△MFC和△NEF中,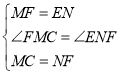 ,
,
∴△MFC≌△NEF(SAS),
∴FE=FC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
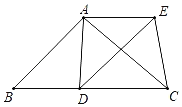
【题目】如图,在△ABC中,AB=AC,点D在边BC上,联结AD,以AD为一边作△ADE,满足AD=AE,∠DAE=∠BAC,联结EC.
(1)求证:CA平分∠DCE;
(2)如果AB2=BDBC,求证:四边形ABDE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
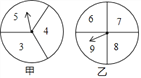
(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
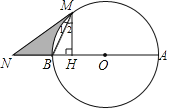
【题目】如图,AB是⊙O的直径,NM与⊙O相切于点M,与AB的延长线交于点N,MH⊥AB于点H.
(1)求证:∠1=∠2;
(2)若∠N=30°,BN=5,求⊙O的半径;
(3)在(2)的条件下,求线段BN、MN及劣弧BM围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
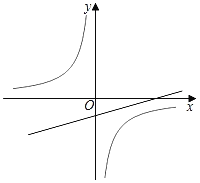
【题目】如图,在平面直角坐标系中A为直线y=![]() x﹣1上一点,过原点O的直线与反比例函数y=﹣
x﹣1上一点,过原点O的直线与反比例函数y=﹣![]() 图象交于点B,C.若△ABC为等边三角形,则点A的坐标为_____.
图象交于点B,C.若△ABC为等边三角形,则点A的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
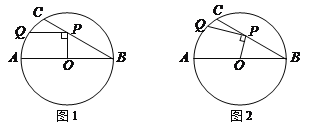
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com