
【题目】(阅读资料)
同学们,我们学过用配方法解一元二次方程,也可用配方法求代数式的最值.
(1)求4x2+16x+19的最小值.
解:4x2+16x+19=4x2+16x+16+3=4(x+2)2+3
因(x+2)2大于等于0,所以4x2+16x+19大于等于3,即4x2+16x+19的最小值是3.此时,x=﹣2
(2)求﹣m2﹣m+2的最大值
解:﹣m2﹣m+2=﹣(m2+m)+2=﹣![]()
因![]() 大于等于0,所以﹣
大于等于0,所以﹣![]() 小于等于0,所以﹣
小于等于0,所以﹣![]()
![]()
小于等于![]() ,即﹣m2﹣m+2的最大值是
,即﹣m2﹣m+2的最大值是![]() ,此时,m=﹣
,此时,m=﹣![]() .
.
(探索发现)
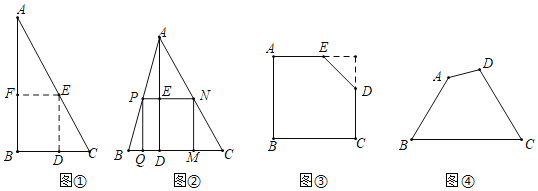
如图①,是一张直角三角形纸片,∠B=90°,AB=8,BC=6,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大.下面给出了未写完的证明,请你阅读下面的证明并写出余下的证明部分,并求出矩形的最大面积与原三角形面积的比值.
解:在AC上任取点E,作ED⊥BC,EF⊥AB,得到矩形BDEF.设EF=x
易证△AEF∽△ACB,则![]() ,
,![]() ,
,![]() ,
,![]() …
…
请你写出剩余部分
(拓展应用)
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),该矩形的面积为 .(直接写出答案)
(实际应用)
如图④,现有一块四边形的木板余料ABCD,经测量AB=70cm,BC=108cm,CD=76cm,且∠B=∠C=60°,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,该矩形的面积为 .(直接写出答案)
【答案】(探索发现)详见解析;( 拓展应用) ![]() ;(灵活应用) 720;( 实际应用) 1458
;(灵活应用) 720;( 实际应用) 1458![]() cm2.
cm2.
【解析】
探索发现:利用配方法解决问题即可;
拓展应用:利用相似三角形构建关于面积的二次函数,再利用配方法解决问题即可;
灵活应用:如图③,延长BA、DE交于点F,延长BC、ED交于点G,延长AE、CD交于点H,取BF中点I,FG的中点K,转化为图②中模型解决问题即可.
实际应用:如图④,延长BA、CD交于点E,过点E作EH⊥BC于点H,转化为图②中模型解决问题即可.
解:探索发现:![]() ,
,
∵![]() ,
,
∴矩形BDEF的面积的最大值为12;
拓展应用:设PN=b,
∵PN∥BC,
∴△APN∽△ABC,
∴![]() =
=![]() ,
,
∵BC=a,BC边上的高AD=h,
∴![]() =
=![]() ,即PQ=
,即PQ=![]() ,
,
∴S=bPQ=![]() =﹣
=﹣![]() b2+bh=﹣
b2+bh=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ≥
≥![]() ,
,
∴S的最大值为:![]() ,即矩形PQMN面积的最大值为
,即矩形PQMN面积的最大值为![]() ,
,
故答案为:![]() ;
;
灵活应用:如图③,延长BA、DE交于点F,延长BC、ED交于点G,延长AE、CD交于点H,取BF中点I,FG的中点K,
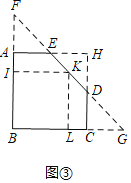
由题意知四边形ABCH是矩形,
∵AB=32,BC
∴EH=20、DH=16,
∴AE=EH、CD=DH,
在△AEF和△HED中,
∵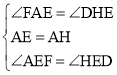 ,
,
∴△AEF≌△HED(ASA),
∴AF=DH=16,
同理△CDG≌△HDE,
∴CG=HE=20,
∴BI=![]() =24,
=24,
∵BI=24<32,
∴中位线IK的两端点在线段AB和DE上,
过点K作KL⊥BC于点L,
由【探索发现】知矩形的最大面积为![]() ×BG×
×BG×![]() BF=
BF=![]() ×(40+20)×
×(40+20)×![]() (32+16)=720,
(32+16)=720,
故答案为720;
实际应用:如图④,延长BA、CD交于点E,过点E作EH⊥BC于点H,

∵∠B=∠C=60°,
∴EB=EC,∵EH⊥BC,
∴BH=HC,
∵![]() =tan60°=
=tan60°=![]() ,
,
设CH=BH=x,则EH=![]() x,
x,
∵BC=BH+CH=108=2x,
解得:x=54,
∴BH=CH=54,EH=54![]() ,
,
∴EB=EC=2BH=108,
∵AB=70,
∴AE=38,
∴BE的中点Q在线段AB上,
∵CD=76,
∴CE的中点P在线段CD上,
∴中位线PQ的两端点在线段AB、CD上,
由【探索发现】知,矩形PQMN的最大面积为![]() BCEH=
BCEH=![]() ×108×54
×108×54![]() =1458
=1458![]() cm2,
cm2,
故答案为1458![]() cm2.
cm2.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
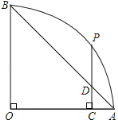
【题目】如图,扇形OAB中,∠AOB=90°.P为弧AB上的一点,过点P作PC⊥OA,垂足为C,PC与AB交于点D.若PD=2,CD=1,则该扇形的半径长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,三个顶点坐标分别为A(0,3)、B(3、4)、C(2,2)(网格中每个正方形的边长是1个单位长度).
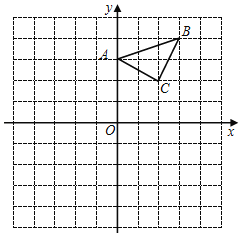
(1)以点B为位似中心,在网格内画出△A′BC′,使△A′BC′与△ABC位似,且位似比为2:1,则点C′的坐标是______;
(2)△A′BC′的面积是_______平方单位;
(3)在x轴上找出点P,使得点P到B与点A距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
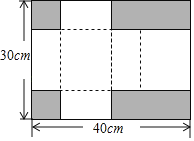
【题目】如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为_____cm3.
查看答案和解析>>
科目:初中数学 来源: 题型:
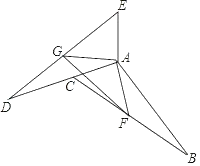
【题目】如图,把△ABC 绕点 A 顺时针旋转 n 度(0<n<180)后得到△ADE,并使点 D 落在 AC 的延长线上.
(1)若∠B=17°,∠E=55°,求 n;
(2)若 F 为 BC 的中点,G 为 DE 的中点,连 AG、AF、FG,求证:△AFG 为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
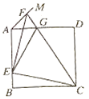
【题目】如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且![]() ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②
,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②![]() 的周长为
的周长为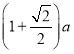 ;③
;③![]() ;④
;④![]() 的面积的最大值
的面积的最大值![]() .其中正确的结论是____.(填写所有正确结论的序号)
.其中正确的结论是____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )
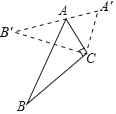
A. 65°B. 60°C. 50°D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,AC=BC=6,∠C=90°.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E.设⊙O交OB于F,连DF并延长交CB的延长线于G.
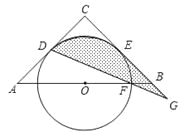
(1)∠BFG与∠BGF是否相等?为什么?
(2)求由DG、GE和![]() 所围成的图形的面积(阴影部分).
所围成的图形的面积(阴影部分).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com