
农民张大伯为了致富奔小康,大力发展家庭养殖业,他准备用40米长的木栏围一个矩形的养圈,为了节约材料,同时要使矩形面积最大,他利用了自己家房屋一面长25米的墙,设计了如图一个矩形的养圈.
(1)请你求出张大伯设计的矩形羊圈的面积;
(2)请你判断他的设计方案是否使矩形羊圈的面积最大?如果不是最大,应怎样设计?请说明理由.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x小明掷B立方体朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P落在已知抛物线y=﹣x2+4x上的概率为( )
A.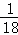 B.
B.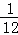 C.
C.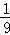 D.
D.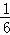
查看答案和解析>>
科目:初中数学 来源: 题型:
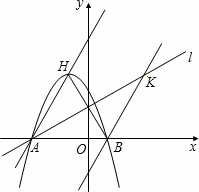
已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: 对称.
对称.
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式;
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)先化简,再求值:2(a+b)+4(2a﹣b)﹣(a﹣b),其中a=﹣1,b=2.
(2)已知代数式x2+bx+c当x=1时它的值为2,当x=﹣1时它的值为8.求b,c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
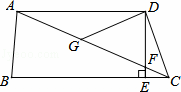
A. 2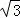 B.
B.  C. 2
C. 2 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com