
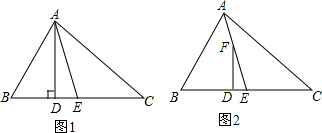
分析 (1)根据三角形内角和定理求出∠BAC,求出∠BAE,根据三角形内角和定理求出∠BAD,代入∠EAD=∠BAE-∠BAD求出即可;
(2)根据三角形内角和定理求出∠BAB,求出∠BAE,根据三角形内角和定理求出∠BAD,代入∠EAD=∠BAE-∠BAD求出∠EAD,推出∠FEM=∠EAD,即可得出答案;
(3)先根据AE平分∠BAC推出∠CAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$[180°-(∠C+∠B)],再根据外角的定义求出∠FED=∠C+∠CAE,然后利用直角三角形的性质求出∠EFD=90°-∠FED.
解答 (1)∵三角形的内角和等于180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠C-∠B),
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B,
∴∠EAD=∠BAE-∠BAD=$\frac{1}{2}$(180°-∠B-∠C)-(90°-∠B)=$\frac{1}{2}$∠B-$\frac{1}{2}$∠C;
(2)(1)中结论还能成立,如图2,过A作AM⊥BC于M,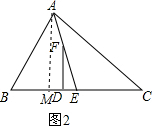
∵三角形的内角和等于180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAB=$\frac{1}{2}$(180°-∠B-∠C),
∵AM⊥BC,
∴∠AMC=90°,
∴∠BAM=90°-∠B,
∴∠EAM=∠BAE-∠BA=$\frac{1}{2}$(180°-∠C-∠B)-(90°-∠B)=$\frac{1}{2}$∠B-$\frac{1}{2}$∠C;
∵AM⊥BC,FD⊥BC,
∴AM∥FD,
∴∠EFD=∠EAM,
∴∠EFD=$\frac{1}{2}$∠B-$\frac{1}{2}$∠C;
(3)(1)中结论还能成立,如图3,
∵AE平分∠BAC,
∴∠CAE=$\frac{1}{2}$∠BAC.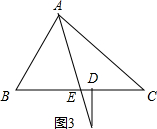
∵∠BAC=180°-(∠C+∠B);
∴∠CAE=$\frac{1}{2}$[180°-(∠C+∠B)];
∴∠FED=∠B+∠BAE=∠B+$\frac{1}{2}$[180°-(∠C+∠B)]=90°+$\frac{1}{2}$(∠C-∠B).
又∵FD⊥BC,
∴∠FDE=90°;
∴∠EFD=90°-[90°+$\frac{1}{2}$(∠C-∠B)]=$\frac{1}{2}$(∠B-∠C).
点评 本题考查了三角形内角和定理,角平分线性质的应用,解此题的关键是求出∠CAE和∠CAD的度数,题目比较典型,求解过程类似.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
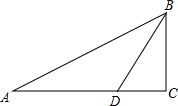 如图,在Rt△ABC中,∠C=90°,BD是∠ABC平分线,BD=10$\sqrt{6}$,BC=15$\sqrt{2}$.求AB和AD的长.
如图,在Rt△ABC中,∠C=90°,BD是∠ABC平分线,BD=10$\sqrt{6}$,BC=15$\sqrt{2}$.求AB和AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
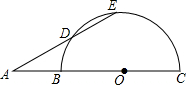 在半圆中,BC是直径,A是直径CD延长线上的一点,在半圆圆上取一点D,使AD=BO,延长AD交一半圆于点E,试说明$\widehat{CE}=3\widehat{BD}$.
在半圆中,BC是直径,A是直径CD延长线上的一点,在半圆圆上取一点D,使AD=BO,延长AD交一半圆于点E,试说明$\widehat{CE}=3\widehat{BD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com