
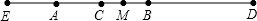
分析 根据线段中点的性质,可得AC的长根据线段和差,可得BD的长,再根据线段的和差,可得ED的长,根据线段中点的性质,可得MD的长,根据线段的和差,可得答案.
解答 解:线段AB长为40mm,C是AB的中点,得
AC=BC=$\frac{1}{2}$AB=20mm.
由CD=3BC,得
CD=3×20=60mm.
由线段和差,得
BD=CD-BC=60-20=40mm.
由BD=2EA,得
EA=$\frac{1}{2}$BD=$\frac{1}{2}$×40=20mm.
由线段的和差,得
ED=EA+AB+BD=20+40+40=100mm.
由线段ED的中点M,得
MD=$\frac{1}{2}$ED=$\frac{1}{2}$×100=50mm.
由线段的和差,得
MC=CD-MD=60-50=10mm.
点评 本题考查了两点间的距离,利用了线段中点的性质,线段的和差,利用线段的和差得出ED的长是解题关键.


科目:初中数学 来源: 题型:填空题
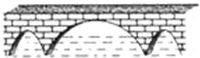 如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20m,顶点距水面6m,小孔顶点距水面4.5m.当水位上涨刚好淹没小孔时,大孔的水面宽度为10m.
如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20m,顶点距水面6m,小孔顶点距水面4.5m.当水位上涨刚好淹没小孔时,大孔的水面宽度为10m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
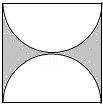 如图,在边长为acm的正方形内,截去两个以正方形的边长为直径的半圆,试用式子表示出图中阴影部分的面积,并求出当a=4时,图中阴影部分的面积为多少?
如图,在边长为acm的正方形内,截去两个以正方形的边长为直径的半圆,试用式子表示出图中阴影部分的面积,并求出当a=4时,图中阴影部分的面积为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
如图所示,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB,点E、F分别是线段AC、BD的中点,CD=4cm,AC+BD=10cm
如图,已知线段AB,点E、F分别是线段AC、BD的中点,CD=4cm,AC+BD=10cm查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
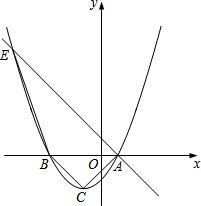 如图,设抛物线y=ax2+x+c与x轴交于两个不同的点A(1,0)、B(m,0),对称轴为直线x=-1,顶点记为点C.且∠ACB=90°.
如图,设抛物线y=ax2+x+c与x轴交于两个不同的点A(1,0)、B(m,0),对称轴为直线x=-1,顶点记为点C.且∠ACB=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com