
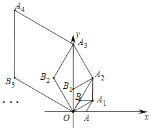
【题目】如图,在平面直角坐标系中,OA=1,以OA为一边,在第一象限作菱形OAA1B,并使∠AOB=60°,再以对角线OA1为一边,在如图所示的一侧作相同形状的菱形OA1A2B1,再依次作菱形OA2A3B2,OA3A4B3,……,则过点B2018,B2019,A2019的圆的圆心坐标为_____.
【答案】(-(![]() )2018,(
)2018,(![]() )2019)
)2019)
【解析】
过A1作A1C⊥x轴于C,由菱形的性质得到OA=AA1=1,∠A1AC=∠AOB=60°,根据勾股定理得到OA1=![]() ,求得∠A2B1A3=60°,解直角三角形得到B1A3=2
,求得∠A2B1A3=60°,解直角三角形得到B1A3=2![]() ,A2A3=3,求得OA3=OB1+B1A3=3
,A2A3=3,求得OA3=OB1+B1A3=3![]() =(
=(![]() )3得到菱形OA2A3B2的边长=3=(
)3得到菱形OA2A3B2的边长=3=(![]() )2,设B1A3的中点为O1,连接O1A2,O1B2,推出过点B1,B2,A2的圆的圆心坐标为O1(0,2
)2,设B1A3的中点为O1,连接O1A2,O1B2,推出过点B1,B2,A2的圆的圆心坐标为O1(0,2![]() ),以此类推,于是得到结论.
),以此类推,于是得到结论.
解:过A1作A1C⊥x轴于C,
∵四边形OAA1B是菱形,
∴OA=AA1=1,∠A1AC=∠AOB=60°,
∴A1C=![]() ,AC=
,AC=![]() ,
,
∴OC=OA+AC=![]() ,
,
在Rt△OA1C中,OA1=![]() ,
,
∵∠OA2C=∠B1A2O=30°,∠A3A2O=120°,
∴∠A3A2B1=90°,
∴∠A2B1A3=60°,
∴B1A3=2![]() ,A2A3=3,
,A2A3=3,
∴OA3=OB1+B1A3=3![]() =(
=(![]() )3
)3
∴菱形OA2A3B2的边长=3=(![]() )2,
)2,
设B1A3的中点为O1,连接O1A2,O1B2,
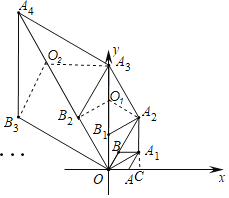
于是求得,O1A2=O1B2=O1B1=![]() =(
=(![]() )1,
)1,
∴过点B1,B2,A2的圆的圆心坐标为O1(0,![]() ),
),
∵菱形OA3A4B3的边长为3![]() =(
=(![]() )3,
)3,
∴OA4=9=(![]() )4,
)4,
设B2A4的中点为O2,
连接O2A3,O2B3,
同理可得,O2A3=O2B3=O2B2=3=(![]() )2,
)2,
∴过点B2,B3,A3的圆的圆心坐标为O2(﹣3,3![]() ),…以此类推,菱形OA2019A2020B2019的边长为(
),…以此类推,菱形OA2019A2020B2019的边长为(![]() )2019,
)2019,
OA2020=(![]() )2020,
)2020,
设B2018A2020的中点为O2018,连接O2018A2019,O2018B2019,
求得,O2018A2019=O2018B2019=O2018B2018=(![]() )2018,
)2018,
∴点O2018是过点B2018,B2019,A2019的圆的圆心,
∵2018÷12=168…2,
∴点O2018在射线OB2上,
则点O2018的坐标为(﹣(![]() )2018,(
)2018,(![]() )2019),
)2019),
即过点B2018,B2019,A2019的圆的圆心坐标为:(﹣(![]() )2018,(
)2018,(![]() )2019),
)2019),
故答案为:(﹣(![]() )2018,(
)2018,(![]() )2019).
)2019).


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
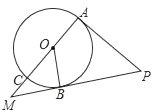
【题目】如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
(1)求证:PB是⊙O的切线;
(2)当MB=4,MC=2时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 随机抛掷一枚均匀的硬币,落地后反面一定朝上。
B. 从1,2,3,4,5中随机取一个数,取得奇数的可能性较大。
C. 某彩票中奖率为![]() ,说明买100张彩票,有36张中奖。
,说明买100张彩票,有36张中奖。
D. 打开电视,中央一套正在播放新闻联播。
查看答案和解析>>
科目:初中数学 来源: 题型:
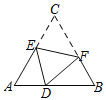
【题目】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上,则CE:CF=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接GA、GB、GC、GD、EF,若∠AGD=∠BGC.
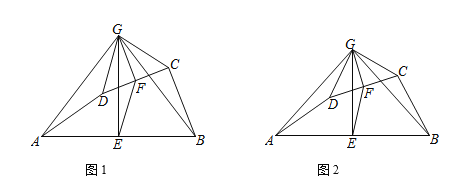
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AB上,以AD为直径的⊙O与边BC相切于点E,与边AC相交于点G,且![]() =
=![]() ,连接GO并延长交⊙O于点F,连接BF
,连接GO并延长交⊙O于点F,连接BF
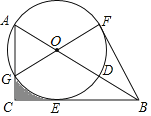
(1)求证:①AO=AG,②BF是⊙O的切线.
(2)若BD=6,求图形中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”.某市加快了廉租房的建设力度,2013年市政府共投资3亿元人民币建设了廉租房12万平方米,2015年投资6.75亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,问2015年建设了多少万平方米廉租房?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各种图形中,有可能不相似的是( )
A. 有一个角是![]() 的两个等腰三角形B. 有一个角是
的两个等腰三角形B. 有一个角是![]() 的两个等腰三角形
的两个等腰三角形
C. 有一个角是![]() 的两个等腰三角形D. 两个等腰直角三角形
的两个等腰三角形D. 两个等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球
(1)请画树状图,列举所有可能出现的结果
(2)请直接写出事件“取出至少一个红球”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com